Lecture 4: Wave-Particle Duality of Matter

Related Resources

 Lecture Notes (PDF)

• Download this transcript - PDF (English - US)

The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation or view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

PROFESSOR: All right. Let's get started. Why doesn't everyone go ahead and take ten more seconds on the clicker question. All right, and let's see how we did. Alright, excellent job, 86% of you, that's right.

What we had just done a clicker question on is discussing light as a particle and the photoelectric effect, so we're going to finish up with a few points about the photoelectric effect today. And then we're going to try a demo to see if we can convince ourselves that the kind of calculations we make work out perfectly, and we'll do a test up here about half way through class. And we'll also talk about photon momentum as another example of light behaving up as a particle. After that, we'll move on to matter as a wave, and then the Schrodinger equation, which is actually a wave equation that describes the behavior of particles by taking into account the fact that matter also has these wave-like properties.

So, starting back with the photoelectric effect -- yes.

STUDENT: [INAUDIBLE] class last time [INAUDIBLE] notes.

PROFESSOR: Oh, sure. Can one of the TAs maybe come up and hand around anyone that didn't get notes? We have not yet perfected the art of entering and exiting this classroom yet, we're still working on that. Raise your hand if you need notes and we'll make sure we get those to you.

All right, so where we left off with the photoelectric effect was when we first introduced the effect, we were talking about it in terms of frequencies. So, for example, we were talking about a threshold frequency as in a minimum frequency of light that you need in order to eject an electron from a metal surface. What Einstein then clarified for us was that we could also be talking about energies, and he described the relationship between frequency and energy that they're proportional, if you want to know the energy, you just multiply the frequency by Planck's constant.

So, now we can talk about it in different terms, for example, talking about e sub i, which is the incident energy or the energy of the light that comes in, or talking about work function here, and that's just another way to say threshold energy. So, the work function's the minimum amount of energy that's required in order to eject an electron, and most of you understand this relationship here, which is a little bit cut off, but it is all the way on in your notes, and that is what you saw the clicker question on -- how you can figure out, for example, the kinetic energy of the ejected electron by looking at the difference between how much energy you put in and how much energy is required to eject that electron in the first place.

So, in this class we'll be talking about energy a lot, and it's often useful to draw some sort of energy diagram to visualize the differences in energy that we're discussing. So, we do this here for the photoelectric effect, and in terms of the photoelectric effect, what we know the important point is that the incoming photon has to be equal or greater in energy then the work function of the metal. So here we have energy increasing on the y-axis, and you see this straight line at the bottom here is lower down on the graph, and that's the energy of a bound electron, so that's going to be a low stable energy.

But we see if we have a free electron, as we do in this dotted line here, that's going to be a higher energy that's less stable. So, if we want to go from that stable state to that less stable state, we need to put in a certain amount of energy to our system, and that's what we define as the work function here -- that difference between the free electron and the electron bound to the metal.

So, the most basic case to understand, which is what we just saw is a case where we have the incident energy coming in, and that incident energy is greater than the work function, and in that case what we see is that we have an electron that is ejected. That makes sense and it also makes sense that this little extra bit here, that's the amount of energy that we have that goes into the kinetic energy of the electrons. So, that's how we could also graph figuring out the kinetic energy.

So, in the second case what we have is what happens if we have the incident energy at some amount that's less than the work function, and in this case we're showing 1/2 of the work function. So in this case, we don't have enough energy to eject an electron, so, an electron is not ejected. And that's pretty clear, too, and the question I want to pose to you is instead the third case here. So in the third case what I'm showing is that we have -- now we're not just talking about 1 photon, we're talking about 3 photons -- let's say we shoot them all at the same time at our metal, each of them having some energy that's let's say 1/2 the work function. So, just to take a little bit of an informal survey, who thinks here that we will have an electron that is ejected in this case?

So a couple hands, all right. And what about who thinks that we will not have enough energy here?

All right. We've got a big majority, and both are logical ways of thinking, but it turns out that the majority is correct, which is not always the case, but the electron is not ejected in this case. And the reason for this, and this is a very important point about the photoelectric effect, and the point here is that the electrons here are acting as particles, you can't just add those energies together. One individual particle is being absorbed by the metal and exciting an electron. So, having other particles around that have the same energy that you could technically add up if you were adding them up like a wave, you can't do the same thing with particles, they're all separate. So, the take-home message is whether you have three photons or 3,000,000 photons that you're shooting at your metal, if you're not at that minimum frequency or that minimum energy that you need, nothing is going to happen.

So, you might ask then well what is the significance of shooting different amounts of photons at a metal? Is there any significance at all, for example, in the number of photons that are hitting the metal or being absorbed by the metal. And there is a relationship here, and that is that the number of photons absorbed by the metal are related to the number of electrons ejected from the metal. So, in this figure here what I'm actually showing is these little sunshines, which let's say are each one individual photon. So we had six photons going in, so the maximum number of electrons that we're going to have coming out is also six because the maximum scenario that we could have that would maximize the number of electrons is that each one of those photons comes in, excites an electron, ejects it from the surface of the metal. It's important to note, of course though, it's not just the number, it's really important that the energy of each one of these individual photons is, of course, greater than the work function of the metal.

So, that's, in fact, it's that number of photons that we're talking about when we refer to the intensity of light, and the intensity of light is proportional to that number, because when we talk about intensity, really we're talking about the amount of energy that a stream of particles, a stream of photons, has per second. So, if we have a high intensity, we're talking about having more photons per second, and it's important to know also what that does not mean. So it does not mean that we have more energy per photon. This is a really important difference.

Intensity, if we increase the intensity, we're not increasing the energy in each photon, we're just increasing the number of photons that we're shooting out of our laser, whatever our light source is. And when we talk about intensity in terms of units, we usually talk about watts, so if you change your lightbulb, usually you see the intensity in terms of watts. But in terms of SI units, which become much more useful if you're actually trying to use intensity in a problem and cancel out your units, we're just talking about joules per second is what intensity is.

So at this point, you should be able to have all the background you need on the photoelectric effect to solve any type of problem that we throw at you, and you see three on this problem set, and we'll probably give you one more on your next problem set, and the reason we ask you so many questions about the photoelectric effect is because it actually is very similar to ionization energy that we'll talk about later, also problems dealing with photoelectron spectroscopy. So, we want to make sure that this is something the entire class is 100% solid on. Sometimes the questions are worded quite differently, so I just want to sum up here the different ways they could be worded.

For example, if we talk about photons, of course, we also just mean light, sometimes we refer to this as electromagnetic radiation, and there's several ways that you might be asked this in a problem or that you might be asked to answer. Sometimes we might just directly tell you the energy of the photon -- that's probably the easiest scenario, because when we think about work functions those are usually reported in energy. So since that's the easiest scenario, you can probably be sure it's not going to be too frequently that you're just given the energy, right, that might be too easy. So really what we'll probably do is instead either give you the wavelength or the frequency and you'll go ahead and calculate the energy from there.

In terms of talking about the electrons, I wanted to point out that in the book and other places you might see electrons referred to as photoelectrons. That's sometimes confusing for people, because it seems like okay, is it a photon or is it an electron. I just want to clarify that it is an electron. It's called this just because it's an electron that results when an electron absorbs a photon's worth of energy, so thus it's a photoelectron. And if we talk about electrons or photoelectrons, again we can describe it in terms of energy, we can talk about velocity, and from there, of course, you can figure out the energy from 1/2 m v squared, and actually we can also describe the electron in terms of wavelength.

So you don't actually know this yet from this class, you'll know it by the end of the class that electrons can, in fact, have a wavelength. So once we cover it, it will then be fair game to ask these photoelectron spectroscopy or these photoelectric effect questions using the wavelength of the electron. Also to point out, a lot of times you'll see electron volts instead of joules, this is the conversion factor here just so you all have it in your notes.

All right. So let's test what we, in fact, know about the photoelectric effect, and before we do that actually, we're going to calculate what we would predict, so when we do the demo it will be meaningful and we can tell whether we're successful or not. So hopefully we will be successful. And as I point this out, we now know how to do any kind of photoelectric effect problem, also this means you should be able to go back to Monday's notes where we filled in all those graphs, which were what different scientists were observing when they were measuring either the frequency or the intensity of light that was irradiating different types of metals, and also the number of electrons ejected, and the kinetic energy of those electrons ejected. You should be able to maybe print out a blank copy of those notes from the website and fill in all those graphs -- not for memorizing them, but now just understanding how the photoelectric effect works.

All right. So let's do an in-class problem, and this will be done with zinc. We have a zinc plate up here, and we're going to -- in a minute I'll describe how we can probe if electrons are coming off of it. But we're going to irradiate it with two different light sources. We have a UV lamp right here, which is centered at a wavelength of 254 nanometers. And then since we have my red laser pointer, we will also try with the red laser pointer, which is centered at wavelength of 700 nanometers.

So, there are a few questions that we need to answer first. So we want to see, do we expect to eject electrons off of this metal surface, or do we expect that we don't have enough energy? So that means we're going to need to figure out what is the energy per photon that's emitted by that UV light. Also, what's the energy per photon of this red laser pointer, and then it's also worth trying a calculation dealing with intensity. So let's also try calculating the numbers of photons that would be emitted by this laser pointer, if, for example, we were to use it for 60 seconds and this were a one milliwatt laser.

So, let's do some of these calculations starting first with what is the energy per photon, and let's start with the UV lamp. So we know that energy is equal to Planck's constant times nu, but what we know about the lamp is its wavelength, or the light that's emitted. We know that nu is equal to c over wavelength. So we can figure out the energy of each photon emitted by our UV lamp by saying e is equal to h c over wavelength.

So let's just plug in these numbers here. That means our energy is equal to 6.626 times 10 to the -34 joules times seconds. And then we have c, the speed of light, 2.998 times 10 to the 8 meters per second. And we want to divide all of that by our wavelength, and to keep our units the same we'll do meters. So that's 254 times 10 to the -9 meters.

So hopefully if some of you have your calculators with you, you can confirm the answer that I got, which is that the energy is 7.82 times 10 to the -19 joules. So, remember what we're talking about here is the amount of energy that's in each photon. So if we think about the work function for zinc, and the work function for zinc is 6.9 times 10 to the -19 joules, do we expect that when we shine our UV light on the zinc, we'll be able to eject electrons? What do you think?

Yes. Good. OK, anyone disagree? No, OK and that's correct, because each photon of light actually has more energy than is needed to eject an electron. So, we would expect to see electrons ejected with the UV light source.

So let's now think about using instead the amount of energy per photon in that red laser pointer. So again, we know that energy is equal to h c divided by wavelength, and energy is equal to -- you have written out in your notes what the actual value for h c is, but now our wavelength is 700 times 10 to the -9 meters. And what we end up with for the energy then is 2.84 times 10 to the -19 joules.

All right. So please raise your hand now if you think there'll be sufficient energy to eject electrons from the metal surface? And raise your hands if you think there won't be. OK. Good hand raising technique. Yes. In fact, there is not enough energy in a single photon to go ahead and eject an electron from this zinc surface.

So our last question we ask is what's the total number of photons emitted if we give this given intensity for 60 seconds? So, keep in mind that one milliwatt is just the same as saying 1 times 10 to the -3 joules per second. So we have 1 times 10 to the -3 joules per second, and we want to multiply that by -- or cancel out how much energy we have per photon, first of all, so how much energy do we have per photon if we're talking about the red laser pointer?

Right. So this value right here. So for every photon we have 2.84 times 10 to the -19 joules. We're saying let's do this for 60 seconds. So what we end up with for the number of photons in this laser beam of light is 2.1 times 10 to the 17 photons.

So this gives you a little bit of an idea of just how many individual photons there are in a laser beam of light. This is a huge number of photons. So the question is does this matter? How about if we shoot this many photons? Does it make any difference at all in terms of whether we can eject an electron? No, it actually doesn't. It is an impressive number, it is very, very large, but it doesn't make a difference. So we see that we do not eject electrons in the case of the laser pointer, even if we have this intensity, even for 60 seconds -- it is still not related to the energy of an individual photon, so we won't see an effect.

All right. So let's hope that we can confirm our predictions here by actually doing it, and Professor Drennen well help me out by loading up our device with electrons, and I'll explain exactly what our set up here is as she does that.

So basically what we have is this zinc plate here. So that's what we want to load up with electrons, and then see if we can remove some. But that's a little bit hard, we aren't all that good at seeing electrons with our eyes, so we need to think of a way to do this. So what she's going to do is start loading up the electrons, and you see this wand here move slowly, and it takes a while to do it, start become perpendicular.

The reason for that is because all of this is connected, so we're moving electrons everywhere in the system. And since we have two bars that are together like this, once they're both loaded up with electrons there's going to be negative charges that repel, so the electrons will want to get as far away as possible, and they're on their slow way to doing that, to getting as far away from each other as possible. And if we do, in fact, hit it with light to get the electrons off, it will go back to the straight up in position, or if it gets knocked hard enough it does that, too. Sometimes it's easier actually not touch it to the metal, I should have--

TA: It's hard to see if it's moving or not.

PROFESSOR: So, our technology TA is also our paper TA. Darcy will hold up the yellow paper. Right, there we go, now we're making a little progress.

TA: It was moving before, you just couldn't see it.

PROFESSOR: So, does anyone have any questions about the set up here, does it make sense what we're looking for the bar to go back once we make some progress. This demo works wonderfully in the winter months in Boston when we will all be full of static at all times. We're still close enough to the summer that the air is not just filling us up with extra static electricity, so it's a little more challenging here. We'll try to make this happen only once. I think that's probably, if we can get one more.

So, it works, I think it's just getting too much [INAUDIBLE]. Sometimes it helps to not actually hit the metal, just put it next to the -- there we go. I wonder if there's some UV light out of this new lighting set up in our classroom here. That would be a little tricky. All right. I think this -- if this sticks. Yeah, it's the pressure of the paper. I think that's good enough, we'll be able to see. If you can keep showing that, though, Darcy, we'll try different scenarios and I'll try not to put laser in your eye. Actually you can look down as well as an added precaution. OK, let's try it with that. That's enough then.

So, the first thing we're going to try is with the red laser pointer, because that we are expecting not to have an effect, and that will prevent Professor Drennen from having to charge up our apparatus again. So, Darcy will look down at this moment and we will hit this with the laser pointer, and what we see is nothing is happening at all. OK, good. Control one working.

So now very carefully take our UV light source -- Darcy again will divert her eyes and her skin. Let me make sure this is actually on. OK, so we've got UV light here, and let's see what we can see, and we lose electrons, if that's what's happening. And it often doesn't go all the way, because actually this device gets stuck right there. So let's charge it up again and see if we can check again. But did you see movement? Are you buying our story here?

This is actually very representative of when you do research in the laboratory, you will find often things do not work quite exactly as they worked 20 minutes ago when you just checked it in your office, for example. And sometimes it's a matter of factors that you need to figure out what it is, and maybe it's that there's extra light in the room we don't know about. It might just be -- so, we did get it back to the starting position. Next time maybe we'll charge it up before class.

All right. So we kind of saw what was happening here, you saw it move a little bit. They'll keep trying to get it going, but maybe we should move on with our lives here while this is happening, and we'll click it back at the end, and if we have a nice set up at any point, I'll just stop and we'll go back and we'll look at it again. Since, I think that's just not going to happen right now.

So let's switch, actually, back to our notes. So, ideally what we did see was, in fact, it does have enough energy with the UV lamp, it wasn't a dramatic shift you saw because we didn't start very high and then it went to that stuck point. But luckily we had the control of the red laser pointer where nothing moved at all. So hopefully you're convinced that your predictions worked well and you are able to predict what's going on when you're looking at the photoelectric effect.

So, it turns out that the photoelectric effect is not the only evidence for the fact that light has these particle-like characteristics. And one thing that Einstein put forth is he figured if well, what we're saying is that light is, in fact, a stream of particles, each one of those particles or photons must, therefore, have a momentum. And that's really neat to think about, because photons, of course, are massless particles, they have no mass, so it's neat to think about something that has no mass, but that actually does have a momentum. And the relationship that he put forth is that the momentum is equal to Planck's constant times nu divided by the speed of light, or it's often more useful for us to think about it in terms of wavelength.

So, since the speed of light equals lambda nu, we can say that momentum is equal to h divided by lambda. And there was experimental evidence that came along that supported this, and this is called the Compton scattering experiment, and this was done by Arthur Compton, and basically what he did was he took x-ray light, which had some frequency, which was a very high frequency because it was x-rays, and he shot it at a stationary electron. And what he was able to observe was that the electrons scattered and now had some momentum, and that both the frequency, and therefore, the momentum of the light that he shot in, went down once it was scattered.

So what he's showing here is, first of all, that the light has some momentum and when it hits an electron it can actually transfer some of that momentum to the electron. So the transfer of momentum from a photon to an electron is what was being observed, and it was seen as completely separate evidence to the photoelectric effect that, yes, in fact, light is behaving in these particle-like ways.

So up to this point, before it was really established that yes, light is like a particle sometimes, there was this very strong distinction between what is light and what is matter. And the distinction was when we're talking about light, light is a wave, and when we're talking about matter, well, matter is a particle. And these behave completely separate, they don't overlap at all in terms of behavior, but then, of course, with the photoelectric effect with Compton's scattering, what we see is that, oh actually, sometimes photons behave as if they're particles. So now this relationship's beginning to get a little bit fuzzy in terms of what is the difference between how we treat light and matter.

And actually, this was taken a step further by Louis de Broglie who in his PhD thesis, as part of his work as a graduate student, put forth the idea that, OK, Einstein says, and everyone agrees that, in fact, light is particle-like at times, and light, in fact, of course has a wavelength, and if it has a wavelength we're saying that it can have momentum. And what de Broglie said is well, if it's true that light, which has a wavelength can have momentum, then it must also be true that matter, which has momentum, also has a wavelength.

And you can look at this in two different ways. One is that he's just re-arranged an equation here and gotten both his PhD thesis and a Nobel Prize, but I think the more representative way to think about this is the real revolutionary idea that he put forth, which is that matter can actually behave as a wave. And in terms of equations that we use, it's sometimes easier to plug in the fact, since momentum is equal to mass times velocity. We can know the wavelength of any matter -- and he's not limiting this, for example, to electrons. What de Broglie is saying we can know the wavelength of any matter at all, as long as we know its mass and it's velocity. And Einstein credited de Broglie, which is a fair statement of lifting a corner of the great veil, because really there was this fundamental misunderstanding about what the difference was between matter and light, and the reality is that they can both be like-particles and they can both show characteristics of waves.

So I mentioned, however, that in terms of de Broglie's work. This was Nobel Prize worthy, absolutely, but it was also his PhD thesis. So, we can think about what would happen if we're on his thesis defense, we're on his thesis committee, we would need to think of some pretty mean, hard, nasty questions to be asking de Broglie about this theory -- that's what happens when you defend your thesis. This is necessary, it's hard to find holes in a Nobel Prize worthy idea. But let's just try maybe one of the basic questions they could ask, and they can say, all right, de Broglie, so you say that all matter, absolutely all matter has wave-like behavior. Why is it that we're never observing this, for example, why is it the table doesn't defract as we bring it through the door? Why don't we see the influence of the wave-like behavior on every day matter?

So it turns out that he could have picked anything to explain this, and hopefully done out the calculation, and we'll do this ourselves. And the example we'll pick is considering, for example, a Matsuzaka fastball. So, many of you are new to the Boston area, now I still realize, and I want to let you know it's not required that you be a Red Sox fan to be at MIT. We do encourage it, however, and in general, I find you don't have to give up that old team, you can keep your old team, even if it's teams I won't name, just keep them to the side. And you can join on to the Red Sox nation on top of that, and part of being a good Red Sox fan is knowing the statistics of your team. For example, if we're talking about a pitcher, like Matsuzaka, we might want to know the speed of his average fastball. We might want to know his ERA. If you're really into it and you're at MIT, maybe you want to know the wavelength of these average fastballs. So, let's go ahead and look at that.

So, if we're trying to figure out the wavelength of a Matsuzaka fastball, we need to consider the velocity first, which is 42 miles per hour. We don't usually do our chemistry calculations in miles per hour, so let's switch that to 42 meters per second, so it's -- sorry, it's 94 miles per hour. And we can use the de Broglie relationship that wavelength should be equal to h over mass times volume. And we can put up here Planck's constant -- and I want to make note that instead of writing joules per second, I actually wrote out with a joule is. A joule is a kilogram meter squared per second squared. Occasionally, you'll find you need to cancel out units, because, of course, you're always doing unit analysis as you solve your problems, and sometimes you'll need to convert joules to kilogram meters square per second squared. We divide that by the mass, so 0.12 kilograms, that's the mass of a regulation baseball for the major leagues, and the velocity of the baseball is 42 meters per second.

So, we can cross out our units doing our unit analysis. The seconds cross out, the kilograms cross out, one of the meters crosses out from the top, so we're left with an answer in meters. It's always good when we're looking for a wavelength that our answer is in a unit of length, that's a good sign already. And what we find out is the wavelength of a Matsuzaka fastball is 1.1 times 10 to the -31 meters.

So, this is really small, this is undetectably small. And especially when we consider it, what tends to be important is the size of wavelength in relationship to its environment. So 1.1 times 10 to the -31 meters is not, in fact, a significant number when we're comparing it, for example, to the length of a ball, or the size of the baseball field. So that would probably be de Broglie's answer for why, in fact, we're not observing the wavelength behavior of material on a day-to-day life.

So, that's for Matsuzaka, and even if you don't memorize all the wavelengths for all the pitchers. I would expect, whether you're a Red Sox fan or not, you to be able to look at a list of different pitchers and their average velocity for their fastball, and tell me who has the longest or the shortest wavelength. You should all be able to know that relationship.

So why don't we go to a clicker question here, and see if you can tell us this. So we have 4 different pitchers we're showing here -- they all have different strengths. It's not always how fast you throw the fastball, sometimes it's your different styles or the different ways that you decide when to throw what. So, first we have Matsuzaka at 94 miles per hour. So, click one if you think that he's going to have the longest wavelength. Tim Wakefield on the DL right now throws a lot slower, because he has that tricky knuckle ball, he doesn't need to throw as fast. Then we have Beckett who can get up 96 just on a regular old day. And Timlin who is about 91 miles per hour, one of our relievers.

So, why don't you take ten seconds to do that. If you can't decide, Timlin is my favorite ever, so that would be a good back up choice if you forgot the relationship between wavelength and the relationship between speed. It looks like, in fact, people did not forget that relationship, and only 1% of you humored me. So, let's see what the correct answer is, and it is, in fact, Wakefield, right, because there's an inverse relationship between how fast a particle is going and what its wavelength is.

So, in terms of wavelength, Wakefield has the largest wavelength, but in terms of being significant, we're still not even close. It's still undetectably small.

Yes.

STUDENT: Why doesn't wavelength go to infinity as it stops, like a standing [INAUDIBLE].

PROFESSOR: As it stops. So, let's think. I would think that it would approach inifinity, and I would need to think about it and get back to you in terms of why we don't actually hit it and see something with an infinite wavelength. I'm sure there's some upper limit as there are to most things, like if we think of wavelengths and different types of light, there is so large that you can get, but you would be approaching that level.

All right. So we can switch back actually to our notes here -- oh, do we have--? OK. We're going to just try this one more time just so you can see it. It'll still likely get stuck in that spot, but we'll just show you one more time the effects of the UV light, and actually we'll throw in an extra trick here, too. We know that UV light gets absorbed by glass, so it shouldn't be able to go through the glass. So first if Professor Drennen can try it through the glass, and we see nothing's happening. Let's move the glass away. All right.

[APPLAUSE]

PROFESSOR: All right. Good. So we can fully believe what our calculations were now, which is a nice thing to do.

Let's go back to considering the wavelengths of different objects. We considered a baseball, but let's also think about now an electron. And an electron is something where, in fact, we might be able to, if we calculate it and see how that works out, actually observe some of its wave-like properties. So, if we do this calculation for an electron, saying it moves at 10 to the 5 meters per second, then what we end up with for a wavelength is 7 times 10 to the -9 meters. A lot of times we talk about these kind of distances either in nanometers or in angstroms so we can say this is 70 angstroms. So this is, first of all, even just on an absolute scale, this is way, way larger than the wavelengths we're talking about for baseball. In addition, if we compare this to the diameter of an atom, which is on the order of somewhere between one and ten angstroms, now we're seeing that, in fact, this wavelength is significantly larger than its environment. So certainly we would expect to see that it has an effect in terms of seeing its wave-like properties.

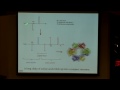
And this was experimentally validated, hopefully, even more clearly than our experiment here. And at first this was done by Davidson and Germer, and they were American scientists who tried defracting electrons from a nickel crystal. They did this in Bell Laboratories, and they found that, in fact, the electronis did defract. And G.P. Thompson showed a similar thing. What he did was he defracted electrons through a very thin gold foil, and this is a picture -- oops, that is not. OK. It is a picture from your book here showing the defraction pattern of an electron going through that gold foil. So, you can see that, in fact, it's confirmed that an electron can have both wavelength and particle-like behavior. And it turns out that Davidson and Thompson shared a Nobel Prize for this discovery of seeing the wave-like behavior of electrons.

So, this is actually kind of neat to point out, because we all remember J.J. Thomson from our second lecture, and J.J. Thomson got a Nobel Prize in 1906 for showing that electrons exist in that they are particles. And it turns out that G.P. Thompson, well, that's his son, so we can actually think of this -- and I'm sure this wasn't the case, but I like to think of it as a little bit of child rebelling against the father. So, the father gets a Nobel Prize for showing that an electron is a particle, and the son says, well, what can I do to top that? I'm going to show the exact opposite. I'm going to say that an electron's a wave no matter how much my father says differently, and I'm going to get a Nobel Prize for that, and he does. But the nice part of the story is, it turns out they're both right. An electron is a particle, but an electron's also a wave. So, father and son, happy ending, they both have their Noble prizes.

So, what happens now that we, in fact, know that matter is a wave? Well, this allows us to try to go back and explain some phenomena that over the years, mounting evidence was building that couldn't be explained. So, for example, when people, and we'll talk about this next class, were looking at different characteristics spectra of different atoms, what they were seeing is that it appeared to be these very discreet lines that were allowed or not allowed for the different atoms to emit, but they had no way to explain this using classical physics. And it turns out that the Schrodinger equation is an equation of motion in which you're describing a particle by describing it as a wave. So you're basically having a wave equation for a particle, and for our purposes we're talking about a very particular particle. What we're interested in is the electron. So basically describing electrons by their wave-like properties.

And this is Erwin Schrodinger, and this is the equation that he put forth where we have h hat psi being equal to e psi. So, let's explain what these are. So this symbol here is actually what we call a wave function. That doesn't mean a whole lot in itself, it will mean more in about two lectures from now. But right now, what I want you to be thinking of a wave function as is just some representation of an electron. So, it's some way of describing an electron. Specifically, we'll talk more about this, it's talking about different orbitals, it's the spatial part of an orbital. But before we get to that, in terms of thinking just think, OK, this is representing my particle, this is representing my electron that's what the wave function is.

This e term here is the energy, or in our case when we talk about an electron in a hydrogen atom, for example, the binding energy of that electron to the nucleus. So, e is binding energy. And h with the carrot or the hat here, well, that carrot or hat tell us it must be an operator, and this is called the Hamiltonian operator. So when you operate on the wave function, what you end up with is getting the binding energy of the electron, and the wave function back out.

When we need to describe the wave function term a little bit more specifically so we can describe, for example, the position of the electron, and I just want to mention that we do have two choices if we're trying to describe this, we could use cartesian coordinates, or we could use polar coordinates where we're either talking about x y z or r theta and phi.

So, I just want to point out that when you look at wave functions, we are going to be using those spherical polar coordinates, and the reason is because a very important interaction here is the interaction between the electron and the nucleus, which we want to describe the distance of in terms of r. So, you can see, it's much easier to describe that as one term, r here, instead of using both y and z.

Another reason I wanted to point this out in terms of the polar coordinates that we're using, is I think they're actually flipped from what you're used to seeing in physics. Sometimes different disciplines have different conventions, which can be very confusing because the whole point of what's happening now is there's so much interplay between different disciplines, but still I think this might be one remaining one where in our case theta is that distance from z, that angle there, where phi is this distance or angle from the x-axis. So just keep it in mind that it's flipped. It turns out we won't really using it, needing to identify it on the graph so much in chemistry. We'll be using the solutions, so you shouldn't have a problem, but I wanted to point it out so it does not look too strange to you.

In terms of the Schrodinger equation, we now can write it in terms of our polar coordinates here. So we have the operation on the wave function in terms of r, theta, and phi and remember this e is just our binding energy for the electron, and we get back out this wave function. So, you might ask, this looks pretty simple up here, right, just with that h hat. It turns out, we can write it out fully. It's three different second derivatives in terms of the three different parameters. It's a little bit complicated. You won't have to solve it in this class, you can wait till you get to 18.03 to start solving these types of differential equations, and hopefully, you'll all want the pleasure of actually solving the Schrodinger equation at some point. So, just keep taking chemistry, you'll already have had 18.03 by that point and you'll have the opportunity to do that.

What I want to point out also is that this h hat, the Hamiltonian operator written out for the simplest case we can even imagine, which is a hydrogen atom where we only have one electron that we're dealing with, and of course, one nucleus. So you can imagine it's just going to get more and more complicated as we get to other types of atoms, and of course, molecules from there.

So, we just want to appreciate that what we'll be using in this class is, in fact, the solutions to the Schrodinger equation, and just so you can be fully thankful for not having to necessarily solve these as we jump into the solutions and just knowing that they're out there and you'll get to solve it at some point, hopefully, in your careers.

So, we'll pick up with that, with some of the solutions and starting to talk about energies on Friday.

Free Downloads

Video

• iTunes U (MP4 - 99MB)
• Internet Archive (MP4 - 99MB)

Free Streaming

• VideoLectures.net

Subtitle

• English - US (SRT)