Lecture 10: Covalent Bonds

Related Resources

Lecture Notes (PDF - 1.6MB) 

• Download this transcript - PDF (English - US)

The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation or view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

PROFESSOR: All right. It's 12:05, so why don't you go ahead and take 10 more seconds on the clicker question today. This is about the periodic trends that we discussed on Wednesday. So specifically, what we're asking here is as we go across the periodic table, we want to consider which has the smaller ionization energy. All right. So, let's focus our attention up here now, whether it's between aluminum or whether it's between phosphorous. And I also wanted you to identify why it's also important to understand why we have these trends, not just to memorize the trend itself.

So, it turns out that the majority of you got the correct answer, which is that it's aluminum. The reason it's aluminum is because aluminum has a lower z effective, so it's not being pulled in as tightly by the nucleus, and if it's not being pulled in as tightly, you're going to have to put in less energy in order to ionize it, so that's why it's actually going to have the smaller ionization energy.

So it looks like not too many more than half of you got this correct, so make sure you can look at your periodic table and figure out how to think about ionization energy in terms of z effective, not just in terms of memorizing what that trend is.

All right, so we can go to today's notes, and in terms of the notes, what we're going to start with is finishing material that's going to be relevant for exam 1, and I told you on Wednesday that actually I'd give you some information today in terms of what you need to do to prepare for exam 1. So you should have gotten two handouts as you came in, and if you didn't, please raise your hand and a TA will come to you and get you that second handout. But the second one says "exam instructions and logistics." So, if everyone can pull that out.

So this is going to tell you pretty much everything you need to know in terms of getting ready for the exam, which is next Wednesday. So when you go home today or some time this weekend, make sure you read this page in detail. I'm just going to go over a few of the main points here.

So, the first is that what we're going over notes today and also on Monday, the exam material ends at the end lecture notes from lecture 9. So that was Wednesday's class -- not at the end of Wednesday's class, but at the end of the lecture notes. So we're going to finish up with those today. I'll be really, really clear when we get through them, and that's where you can stop in terms of studying for this.

Also, on everything that was on problem-sets 1 through 3. So, you turned in p-set 3 today, but we'll have the answers posted for you this afternoon, so you can start studying from p-set 3, even as early as tonight, if you want to, because those answers will be there for you.

So, in terms of what it is that you need to prepare and bring with you for the exam, you need to bring your MIT ID, especially if you haven't been showing up regularly to your recitations and you aren't 100% sure if your TA knows exactly who you are, you need to make sure you have your MIT ID with you. You can't take the exam unless you're registered for the class, and we need to make sure we can verify that.

You also need to bring a calculator, of course, because we'll be solving problems that involve calculations. You can bring any calculator you want, we don't actually have restrictions for calculator types here, but what you can't do, is you can't program any relevant chemical or information about constants in there. It's OK to use certain fundamental constants that come in a lot of calculators, so there's nothing we can do about that. That's OK. If you're wondering what's OK or what's not OK, it's very clearly written out in this handout, so make sure you read through it, because it is your responsibility to make sure that your calculator does not have anything extra programmed in it. And if you have your calculator all set up as you love and you don't want to change it, then maybe you should just go and get an $8.00 scientific calculator that doesn't have any of the graphing functions, because you don't actually need them, so that's a better option for you, you can do that as well.

And I had mentioned several times that you do not need to memorize the majority of the equations and you don't need to memorize any physical constants. So if you flip the info page over on the back here, what you'll see is the periodic table, this is the same one that I've handed out in the last two lectures -- the periodic table without any electron configurations. This is exactly the sheet here, it's exactly what you'll get on exam day. You'll also see that they have all the physical constants that you're going to need, and also a bunch of the actual equations that we've been using in the first couple weeks here. So you don't need to memorize any of this, you're actually going to be handed this. There are a few equations that you need to memorize -- those are the very simple -- very, very simple equations, such as e equals h times nu -- hopefully you don't have to sit down and try to memorize that, hopefully we all know that already. But just to be really clear, I've written out exactly which equations you do have to memorize on the front here, so long as you know those, the rest you can just look up.

And in terms of using these equations in solving problems on the exam, and also using these constants, make sure if you think there might be any chance you're going to get any little part of a problem wrong or do a calculation inaccurately, you need to write out every single step of your thinking as you write out these problems. We can't give you any partial credit whatsoever if we can't see your thought process. So it's important to write out the equation you use, you need to write out the constants that you use to fill in that equation. And that we need to see your work to get full credit, and then especially if you get things wrong, we need to know where it went wrong, because we do try to give as much partial credit as possible in these exams, since there are a lot of places where small mistakes can result in the wrong answer.

So also, along those lines in terms of test taking, make sure you also box your answers and that you keep track of significant figures and that you also remember to include your units. These are just little things that can add up, so you just want to make sure you're on top of those. And your TAs on Tuesday are going to share a lot of other types of sort of exam strategies in thinking about how you can approach an exam when we're in a time situation like we are, so they'll share some of their experience with you in terms of taking these timed exams.

So, in terms of practicing this weekend, I mentioned that instead of getting a problem-set today, what I am going to be posting is optional extra problems. So they're optional, but they're very, very, very highly encouraged that you do these, because this is going to give you practice for the types of problems that are going to be on the exam. We're also posting a practice exam for you to take, so after you're completely done your studying, it's good to have everything done before you take the practice exam, and then sit down just with this sheet here and your calculator, and ideally a timer, and make sure you can do the practice exam in the allotted amount of time. So that way you can have an idea if, oh, I do really understand this but I'm a little bit slow, maybe I need to practice this one type of problem a little bit longer so I can get up to speed so I'm going to be able to get through all this in terms of the exam time.

All right. So let's move on to today's topics. So, as I said, we're finishing up with what we left off with yesterday -- or excuse me, on Wednesday. This includes atomic radius and the idea of isoelectronic atoms. So that's going to be the end of the exam 1 material, and then we'll move on to exam 2 material, which is kind of exciting, because we've been talking about just individual atoms and ions up to this point, and now we can talk about molecules, so we're going to start talking about bonding. So for some you that are less interested in maybe the physical structure of an individual atom, now some more exciting material for you might be coming up if you like to think about how, instead, molecules behave, either within bonding, within themselves, or with other molecules, that's what we're going to be heading to in this next unit.

So, we need to finish up with periodic trends. And first, on your lecture notes, I start with atomic radius. I was so proud of myself getting the lecture notes finished early and handing them in to CopyTech, and then I realized we didn't do electronegativity on Wednesday.

So, if you can flip your lecture notes over and just write on the blank space, we're going to cover electronegativity first here, and specifically, you can go back and fill this in to your lecture 9 notes, if you want to stay organized, but I just suggest just writing it on lecture 10 notes now and going back. You can still keep organized, which hopefully most of you like to do, and get it in the right place in the notes.

So, when we're talking about the idea of electronegativity, essentially what we're talking about is the ability for an atom to attract electron density from another atom. So it's just a measure of how much does one given atom want to pull away electron density from, let's say, an adjacent atom.

So it's actually very related to what we're talking about when we said electron affinity, and it's also related to ionization energy, and we can call electronegativity by symbol here, and it turns out that it's going to be proportional to 1/2 of the electron affinity of a given atom, plus the ionization energy. So, in other words, we can just think of electronegativity as being the average of that ionization energy and the electron affinity. This should make sense, because if an atom has a very high electron affinity, that means it's really happy taking an electron from another atom, or taking a free electron -- that that's very favorable. If something has a high ionization energy, it means that it really, really, really does not want to give up an electron. So you can think about how these 2 things combined are going to be electronegativity, which is a measure of how much an atom wants to pull electron density away from another atom.

So, if we think about electronegativity as a periodic trend, we can just draw our nice periodic table here, and let's separate it into quadrants. So if we think about the upper right hand part of the quadrant, well, this is where we're going to have high electron affinity and high ionization energy, so we're also going to see high electronegativity here. And in contrast, in the lower left hand part of the periodic table, these 2 quantities are low, so also what we're going to see is low electronegativity.

And if we talk about what's going on in areas, or with atoms that have high electronegativity, and we think about whether they're electron donors or electron acceptors, what would you expect for an atom that has high electronegativity? Is it going to be an electron donor or acceptor? Great. Yup, it's going to be an electron acceptor, it wants to accept electrons, it wants to accept electron density.

So, in contrast, if it has a low electronegativity, this then is going to be an electron donor.

All right, so it's very common to talk about electronegativity of different atoms, and you can look up tables of these. Often what you'll see is not a table based on this definition, but something that's called the Pauling definition of electronegativity, but it's exactly the same idea and the same trend as this more numerical way to think about what the meaning of electronegativity is.

All right, so now we can move on to the start of today's notes, which is atomic radius. So this, in fact, is going to be our last principle that we're going to talk about in terms of periodic trends. So this is actually the most straightforward, so sometimes it's nice to end with the easiest concept, and that's what we're doing here. And if we're talking about atomic radius, essentially we're talking about atomic size. And immediately it should probably come into your head that we don't actually have an atomic radius that we can talk about, right? What I just spent many lectures discussing is the fact that we can not know how far away an electron is from the nucleus, so we can't actually know the radius of a certain atom. And that's true. An atom's not a defined sphere, for example. We can't define it as an exact radius in terms of the definition we might think of classically. So, keep that in mind when we're talking about atomic radius, I'm not suddenly changing my story and saying, yes, we do have a distinct radius. Instead, what people have done is come up with different ways to think about how they can define a radius. And one common way to think about it, is to think about the value of r, or the radius, below which 90% of that electron density is going to be contained. So we're not saying it's all the electron density, it's just 90%. Because we know as we go to infinity, even though the density gets smaller and smaller and smaller, we still have electron density very far away from the nucleus. So, what we're going to define is just let's just capture 90% of that electron density.

So, that's one way to think about it, and there's also another way, and this is the way that your book presents it. If you, in fact, have two of the same atom right next to each other, let's say you have a crystal, or let's say you're talking about a metal, what you can do is just look at the distance between the two nuclei, and split that in 1/2, and take the atomic radius that way.

So, these are two different definitions of how to think about atomic radius, but really what you find when these are measured is they come up with almost the identical values, so there are tables you can look up of atomic radii and see these values, and you can trust them that, yes, they work for both this definition and for this definition here, in most cases.

And what we've been talking about with all of these properties are, of course, how can we figure out what that is for a certain atom by looking at the periodic table, so we want to think about the periodic trend for atomic radius. And we know as we go across a row in the periodic table, what's happening is that z effective or the effective pull on the nucleus is increasing. So would you expect, therefore, as we go across a row for the atomic radius, to increase or to decrease? Good. OK, yes. We are expecting to see that it decreases because it's feeling a stronger pull, all the electrons are being pulled in closer to the nucleus, so that atomic size is going to get smaller.

This is in contrast to what's happening as we go down a periodic table. So as we go down we're now adding electrons to further and further away shells, so what we're going to see is that the atomic radius is going to increase as we're going down the periodic table.

And we can look at an example here. If we start in the upper left hand corner of the periodic table with lithium, you can see that as we go down the table, what you're seeing is that that atomic radius is actually increasing, as we would expect. Whereas, if we go across a row, what we see is that the atomic radius is decreasing.

So, again, this is one of the more straightforward trends. You just need to remember what's happening to z effective, which really tells us what's happening with all the trends, and once you know z effective, you can figure out, for example, what direction the atomic radius should be going into.

So, that's it for periodic trends. We have talked about four different ones. We talked about ionization energy, electron affinity, we talked about electronegativity, which is just kind of a combination of the first two, and then ended with atomic radius here. And what you might have noted is although we described how to make predictions about these properties, I didn't talk too much about what it actually means, what the ramifications of these different properties are. And the reason we didn't do that is because we're actually going to spend much of the rest of the course relating these different properties to the properties of molecules in terms of bonding, and also in terms of chemical reactions.

So, for example, if we have a very electronegative atom within a certain molecule, what you'll actually find is that it does affect how the molecule is going to take part in different chemical or biological reactions. And this will become more and more clear as we actually talk about these reactions and talk about bonding. But you need to be able to predict what kind of properties a certain atom's going to have within a molecule, whether you're talking about something, for example, that's very electronegative, or something that is not electronegative at all, it is going to make a difference in terms of thinking about how molecules are structured and also how they interact with other molecules.

However, I can give you at least one example while we're still on just talking about atoms. So we haven't gotten to molecules yet, we're just talking about single atoms or single ions, but what's nice is just talking about this very straightforward principle of atomic radius. We can already use that in terms of single ions to think about a really complex biological issue, which is to talk about ion channels.

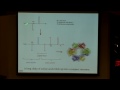
So, that is just a quick example for some of you, you might be very familiar with ion channels, others might not know what these are, so I'll just tell you quite briefly that ion channels are these very massive transmembrane proteins. Essentially, what they are is it's a protein that spans the membrane of a cell. And what they do is they regulate the influx of ions across that cell. So the influx of ions from the outside of the cell to the inside of the cell, for example. And you can think of ion channels as being gated, by gated it means the gate can be closed and no ions are going through, as in this case here. Or you can talk about the gate being open, and in this case, you can see that you will have an influx of ions.

So, ion channels are important for maintaining a voltage difference between the inside of the cell and outside of the cell, and they're found in all sorts of cell types in your body, but if you think about where they're most prevalent, it turns out that they're most prevalent in muscle cells and also in nerve cells, so in your neurons. And essentially, what they do in neurons is they underlie those nerve impulses, or those, essentially what we call electrical signaling between neurons -- you might also call that the action potential of the neurons. So essentially, they regulate this action potential, and they do so by helping to establish and then control the voltage gradient within the cells. so, essentially, they're establishing or controlling or changing the difference between the charge inside the cell and the charge outside cell.

And when we talk about any type of ion channel, there are just tons of different kinds of ion channels, and you can characterize them in a few different ways. So, for example, you could characterize them in terms of how they're gated, and basically how they open or close -- that's one way to talk about different types. Another way to talk about different types is to think about which ion they're selected for. And all ion channels are selective for a single type of ion, and we can think about how that selectivity takes place, and that's where this idea of atomic radius is going to become very important.

So, for example, if we look at sodium channels, and sodium channels are some of the particularly prevalent ones when we're talking about neurons, if you think about the cell membrane, and this little green cartoon is me trying to show a sodium channel here, and in this case, you can see that it's closed, such that no ions are getting through. However, when that gate is opened, the sodium channel is now going to be incredibly selective and only let through sodium ions and no other type of ion. And this is really interesting to think about because you can imagine in our body we have concentrations of all types of ions, and specifically, some seem very, very similar to each other. So we could think about comparing the potassium ion to a sodium ion. They have the same charge of plus one. The only thing that's different is that they're one down on the periodic table, potassium is down one row, so it's going to be a little bigger, but when we're thinking about size, it maybe does not seem that significant to talk about the size. But what we find out is that it is.

So, what happens, this is another view of a sodium channel, so this is actually looking a little bit more at the protein structure. What all of these channels have is what's called a selectivity filter, so this filter filters out the type of ion that's going to be allowed through.

And there's two parts of the filter. First we need to select for actual charge. So the way that it does this is the filter is actually lined with all of this negative charge, and for those of you that are more into biology or biochemistry, that's because of negatively charged amino acid residues, but all you need to think about is that it has negative charge in the inside of this pore, and what happens then is that if something has a positive charge, it's going to be stabilized to enter this pore, whereas any negative ions are going to be repelled.

So that's the first step in being selective, but now how do we differentiate between these sodium and potassium ions. And the answer is just really beautifully simple, and it's just that the pore gets really, really tiny, to the point that it gets so small that all that can fit through this pore is one a single ion, one single sodium ion, solvated by one single water molecule. And that's all that's big enough to pass through or small enough to pass through. And if we go up even just one row on the periodic table to potassium, what we actually see is now that it's going to be too large, and, in fact, a potassium solvated with one water molecule won't go through our channel.

So, this is just one example of how these properties can already, even our understanding just talking about single atoms, can already make an impact in these biological systems. And actually, a question that might come up, I just explained, the sodium channel, you might say, well, how do potassium channels work then, because I can understand how you can filter something big out, but how do you filter out something small. And it turns out that size exclusion is also the principle that's in play with potassium channels as well, but in this case it's a little more complex, because what happens is these negative residues the are in the pore need to stabilize the potassium as it goes through, and the potassium is large enough to make all the contacts it needs, but the sodium, which you can picture being smaller, actually can't reach all of the stabilizing charges that it needs to to get through the pore.

So, again, it is based on size, it's a little bit less intuitive than the idea of just straining out all of the potassium ions. But again, many of these ion channels have this size exclusion pore, it's a very important part of them.

All right, so that was a quick aside on thinking about how these properties can, in fact, relate to something in our body. Let's move on to the last topic in terms of this first exam, which is thinking about the idea of isoelectronic atoms, or isoelectronic ions. And isoelectronic is very straightforward, it just means having the same electron configuration. The easiest way to look at this is just to do an example. So let's take the example of neon. This has the electron configuration of 1 s 2, 2 s 2, and 2 p 6. It looks like we're cut off the screen a little bit here, but you can see I've just circled it there. So we can go ahead and think about, well, are there any other atoms that are going to have the same electron configuration? The answer to that is definitely no -- if they had the same electron configuration, they would, in fact, be neon. But we can think about different ions that have this electron configuration.

So for example, if we think about fluorine, that has an electron configuration of 1 s 2, 2 s 2, 2 p 5, so all we would need to do is add one more electron to get the same configuration as for neon. So if we want to write out what that would be, it would just be to say that f minus is isoelectronic with neon.

So, we can say that -- if we have neon here and we want to think about what's isoelectronic, f minus would be isoelectronic. We also have oxygen -- what would the charge on oxygen be? Um-hmm, right. 2 minus. Then also, nitrogen, 3 minus -- these are all going to be isoelectronic with neon.

We can go in the other direction, so let's go to sodium, but we would need to take away an electron to make it isoelectronic. So we would say sodium plus, or magnesium 2 plus, we can just keep going -- aluminum 3 plus, silicone 4 plus, and we can go on and on in either direction all the way across and down the periodic table.

So, that's the idea of isoelectronic ions. These are all isoelectronic, they all have the same electron configuration.

And we can also think about going back to atomic size for a second. What the relationship is between these ions and their parent atoms. So, for example, if we think of the fluorine minus case, would you expect fluorine minus to be larger or smaller than neutral fluorine? Okay. I heard mostly larger, but a little bit of a mix in there, and it turns out that larger is correct. And we can think about why -- essentially we have fluorine and now we're adding another electron. So you can picture that fluorine is going to get larger in this case. And that would be true for all of the negatively charged ions.

So, by the same logic, that means that all of our positively charged ions are, in fact, going to be smaller in terms of radius, compared to their neutral parents. Not only are we taking away an electron here, but we're also going to decrease shielding, so the electrons that are already in there are going to feel a higher z effective and will be pulling and the atom will be getting smaller.

And this is just a picture showing some of these sizes with their parent. So, for example, a lithium here, you can see how lithium plus is smaller than the actual lithium atom in its neutral state. Whereas for fluorine, fluorine is smaller than f minus is the one that's the outer shell shown here.

So, let's do a clicker question on isoelectronic atoms. And now we're asking you to look at krypton, so the atomic mass is 36. You can actually just grab that handout, the second handout on the exam and look at the periodic table there. So, which of the following ions listed is isoelectronic with krypton? OK, let's take 10 seconds on that.

OK, good. This might be our all-time high, 89% got this right. This is great. So, selenium 2 minus is what's going to be isoelectronic, because if you add two electrons to selenium, you'll get the same electron configuration that you have for krypton here.

OK, I think we can safely go back to notes.

So, I said I would announce it, that's the end of exam 1 material. So, if you compartmentalize things in your brain in certain ways, put that off into the end of the exam 1 part of your brain, and now we're going to move on to exam 2. Remember, for exam 2, you still need to know and understand everything you learned in exam 1, but you can put off learning it completely until we get through, at least, next Wednesday before we start maybe spending time on these concepts outside of class.

So, we're going to start with talking about bonding, and any time we have a chemical bond, basically what we're talking about is having two atoms where the arrangement of their nuclei and they're electrons are such that the bonded atoms results in a lower energy than for the separate atoms. So we know we always want to have our systems in as low an energy as possible, so it makes sense that a bond would happen any time we got a lower energy when we combine two atoms, versus when we keep them separate.

So specifically, today we're going to talk about covalent bonds. A covalent bond is any time we have a pair of electrons that is shared between two different atoms. And the key word for covalent bonds is the idea of being shared. The two electrons, for example, we see in the h 2 molecule, they don't belong to one or the other atom, they're actually shared. And what we'll see later, is that the sharing is not always equal -- in the case of h 2, it is completely equal sharing. In some cases, because of things like electronegativity, one atom will take away more of the electron density than the other atom, but they're still shared, even if they're not always evenly shared.

So, in talking about covalent bonds, we should be able to still apply a more general definition of a chemical bond, which should tell us that the h 2 molecule is going to be lower in energy than if we looked at 2 separate hydrogen atom molecules. So, let's see if that's actually the case. So if I tell you that the energy for single hydrogen atom is negative 13 12 kilojoules per mole. If we want to talk about two hydrogen atoms, then we just need to double that, so that's going to be negative 2 6 2 4 kilojoules per mole that we're talking about in terms of a single hydrogen atom.

So, let's compare this to the energy of the h 2 molecule, and we find that that's negative 3,048 kilojoules per mole. So, in fact, yes, we did confirm that these covalent bond, at least in the case of hydrogen, we have confirmed by the numbers that we are at a lower energy state when we talk about the bonded atom versus the individual atom.

And when we talk about covalent bonds, there's 2 properties that we'll mostly focus on, and that's going to be thinking about the bond strength or the energy by which it stabilized when it bonds. And we can also talk about the bond length, so we might be interested in what the bond length is, what the distance between these two nuclei are. And we can actually better visualize this if we plot how that energy changes as a function of internuclear distance.

And when I say internuclear distance, we actually call this r here. It's kind of ironic that we put this in the same lecture as we talk about atomic radii, which we also call r, but they're two different r's, so you need to keep them separated in terms of what you're talking about. When we're talking about r for internuclear distance, we're talking about the distance between two different nuclei in a bond, in a covalent bond.

So, if we look at this graph where what we're charting is the internuclear distance, so the distance between these two hydrogen atoms, as a function of energy, what we are going to see is a curve that looks like this -- this is the general curve that you'll see for any covalent bond, and we'll explain where that comes from in a minute. I want to point out that the zero energy is defined as when you have a naked proton where the electron has popped out -- that's what we've defined as zero energy up to this point when we're talking about single atoms. So, for starters we'll keep that as our zero energy, we're going to change it soon to make something that makes more sense in terms of bonding, but we'll keep that as zero for now. So, we see that the two h atoms separate have a certain energy that's lower than when the electron's not with the atom. And then even lower down, we have our bonded hydrogen molecule.

So, we can think about the different kinds of interactions that are taking place. I said what hold the bonds together, what holds two atoms together is the attractive force we have between each electron and the other nucleus. That's the huge force that we're talking about in terms of making a bond stable, but there are also repulsive forces, so you can imagine we're going to have electron-electron repulsion between the two electrons if we're bringing them closer together. And the real killer is if we get too close we're even going to have nuclear-nuclear repulsion between the nuclei of the two atoms.

So, this makes this chart shown in pink make a lot more sense, because if we're way out at very far distances, essentially what we have here is we're talking about two separate atoms. They're not interacting at all so that's why the energy is the same as that for two individual atoms, that's what we're dealing with. As we get closer together, we start get lower and lower in energy. The reason is because the predominant force at this point is going to be the attraction that's being felt between the nuclei and the electrons in each of the atoms. At some point you're going to hit a well here, which is the point where it's most stabilized or at it's lowest energy. So, when we think about a bond length, this is going to be the length of our bond here, that makes sense because it's going to want to be at that distance that minimizes the energy.

But as we keep getting closer, even though as we get closer, the attraction is going to get stronger between the two nuclei and the electrons. We're also going to start to have the repulsive forces become more prominent here, and, in fact, they take over at some point, becoming the more prevalent of the forces, so as you get closer, the electron-electron repulsions, and eventually the nucleus-nucleus repulsion is going to mean that your energy is just absolutely skyrocketing, so it just keeps going up and up as you get closer to zero here.

So, when we want to talk about the information that we can get out of looking at a chart like this, well, the first thing I did tell you was that this is going to be the bond length, so the distance r where the energy is lowest, but we can also talk about something called dissociation energy, that's going to be this distance right here or the energy that is this value. And the dissociation energy is very intuitive in terms of what it means, it means how much energy you need to put into the molecule in order to disassociate it into its individual atoms. And so we can actually think about how do we calculate what the dissociation energy should be for h 2, so let's go ahead and do this.

So, if we talk about dissociating h 2, we're going from the h 2 molecule, and breaking this bond right in half, so we now have two individual hydrogen atoms here. So we need to take the energy for the two atoms, which we know is -- so let's take our dissociation energy is going to be equal to negative 2 6 2 4 kilojoules per mole, and we want to subtract the energy of the hydrogen molecule itself, so that's going to be negative 3 0 4 8 kilojoules per mole. So, what we get for the disassociation energy for a hydrogen atom is 424 kilojoules per mole.

So what that means is that's how much energy we would have to put in to a hydrogen molecule in order to get it to split apart into its two atoms.

So, another way to talk about dissociation energy is simply to call it bond strength, it's the same thing, they're equal to each other. If we know that this is it the dissociation energy for a hydrogen atom, we can also say the bond strength for hydrogen molecule is 424.

So, there's actually another way to graph it where we can directly graph the dissociation energy or the bond strengths. So I said before when we were talking about single atoms, we always define the zero energy as when an electron was actually ejected, but now, when we talk about chemical reactions taking place, it's very, very rare that we're actually going to be talking about anything that gets to this point here. It's much more relevant to set our zero point energy as the separation of a bond in terms of talking about the reactions that we'll usually be dealing with here. So, let's change our graph where we now have this zero point set as the two individuals hydrogen atoms, and then we see that our h 2 molecule is at the negative of the dissociation energy, or the negative what that bond strength is. So we know what that number would be, it would be negative 424 kilojoules per mole that we see here.

So, what this let's us do now is directly compare, for example, the strength of a bond in terms of a hydrogen atom and hydrogen molecule, compared to any kind of molecule that we want to graph on top of it. So, let's, for example, look at nitrogen. So n 2, we can do the chart here in green, so it's the green dotted line, and what we see is that we have now defined this energy as where the 2 nitrogen atoms are separated. So what we can actually directly compare is the dissociation energy or the bond strength of nitrogen versus hydrogen.

So, if we think about this, which would you say has a stronger bond? Is it going to be hydrogen or nitrogen? Yup, it's going to be nitrogen. And the reason we can see that by looking at this graph is that we see that nitrogen when it's bonded is in an even lower well than we saw for hydrogen. It's going to be a stronger bond because it's more stabilized when it when it comes together as a molecule.

We can also think about the distance, the bond distance. So, which would you say is going to be shorter in this case? Is a hydrogen bond shorter, or is a nitrogen-nitrogen triple bond going to be shorter? Um-hmm, again, we can get this information directly from our graph. We see that the radius is shorter, so that means that the nitrogen-nitrogen bond is going to be shorter.

We can know this information even if we just knew that the bond was stronger, we wouldn't need to look at a graph here, because it turns out that if you have a stronger bond, that also means that you have a shorter bond -- those ywo are correlated. And something that we'll see later on is that triple bonds, for example, are going to be stronger than a corresponding double bond or a corresponding single bond. So, if we talked about a nitrogen-nitrogen single versus double versus triple bond, the triple bond will be the shortest and it will be the strongest.

So, that's basically the idea of how we are going to be thinking about covalent bonds. It's also important, once we start talking about molecules, to have a way to represent them, and also to be able to look at a shorthand notation for a certain molecule and understand what the bond is. So, for example, down here I wrote that it was n 2 and that it was h 2, but when I re-wrote the molecules up here, you saw that it's an h h single bond where it's a nitrogen-nitrogen triple bond. So any chemist should be able to just look at n 2 and know that it's a triple bond, but that's not something that we've learned how did to do yet, so let's go ahead and start a new topic that's going to allow us to have some sort of sense of what the valence electron configuration, which includes whether something's a single or double or a triple bond can be figured out for any given molecule.

So, to do this, what I'm going to do is introduce the topic of Lewis structures. We're going to really get into this next class, but I just want to introduce it to you to give us a start, and many of you have used Lewis structures in high school, but we'll be doing some much more challenging Lewis structures, I can assure you, in this class here.

So, a Lewis structure is basically an organizing property of bonding, of molecules, which is the idea that when we're thinking about bonding, the key is to achieve a full valence shell in each of the individual atoms. So we want to have in an h h bond, for example, a full shell for each of the hydrogen atoms. And G.N. Lewis is the scientist that is credited, and who did, in fact, come up with this idea for the way to represent this, so the other parts of this idea, another way to phrase it is that the electrons are going to be distributed in such a way that we have what are called full octets for each of the atoms, and basically that's the same thing as saying we have a full valence shell, and this is something that Lewis was able to recognize very, very early, way before we had quantum mechanics to describe what these orbitals were, but it makes sense a full valence shell means for most atoms that we have a full s orbital plus a full p orbital, so we're going to have a total of four orbitals that are each filled with eight electrons, so that's why we see that we need an octet here.

And the idea is that when you do these Lewis dot structures, we're representing electrons with dots, which we'll see in a minute, and each dot is going to represent a valence electron. So, hopefully, you remember what we mean by valence electrons versus core electrons. Core electrons are all those electrons held in really tight with the nucleus in the inner shells, whereas the valence electrons are only those electrons that are in the outer-most shell, or at your highest value of n of the principal quantum number. So, Lewis structures are really a model for a way to think about what the valence electron configuration is, and as I said, it's not based on quantum mechanics, it's something that Lewis observed far, far before quantum mechanics were discovered. So he came up with the ideas that led to the idea of Lewis structures in the very early 1900's. So you might ask well, why are we using this model if it clearly doesn't take into account quantum mechanics? And the reason that we use it is that it is incredibly accurate, and allows us to very, very quickly predict and to predict accurately, in most cases, what the electron configuration of molecules are going to be. So this is really useful. We don't always want to go and solve the Schrodinger equation, and in fact, once we start talking about molecules, I can imagine none of you, as much as you love math or physics, want to be trying to solve this Schrodinger equation in that case either. So, what Lewis structures allow us to do is over 90% of the time be correct in terms of figuring out what the electron configuration is.

And we won't just use them in this class. If you actually go to any of the chemistry labs at MIT, if you go over to building 18 and look in the organic labs where they're synthesizing new molecules or making up new reactions, what you'll see if you open anyone's notebook, their lab notebook, assuming they keep a nice lab notebook, is that they will have Lewis structures drawn in there that explain the reactions that they're going to be doing for that day. And I mean this means way past all the chemistry they've taken, they're now graduate students or they're now professors, and they're still writing out Lewis structures. Now they're writing a more abbreviated form, which you'll probably get to if you take organic chemistry, but really it's the exact same idea.

And this goes all the way back to 1902. In fact, Lewis was an American scientist, so he was trained in America, and he actually was a professor here at MIT from 1905 all the way to about 1911 or 1912, and these are some notes from 1902, and you can't see them very well, but this was essentially an early form of Lewis structures, and this was called the cubicle atom. So, basically what he's showing in these cubes is that there are eight spaces that need to be filled up to have a full cube. So in order to fill them, he would have to have eight electrons or an octet around the cubes. So what we're seeing is this is notes from 1902 -- he actually didn't publish any of this work or these ideas that led to Lewis structures until 1916, but his early class notes were used as evidence about how long ago he actually came up with the idea of it.

So it's really neat to think that your counterparts 100 years ago right here at MIT could have been sitting in a class where they had Lewis as their lecturer, and he's putting forth these ideas -- these are actually his lecture notes, even though it wasn't even published yet, and giving this idea of Lewis structure, which is exactly what we keep using today in order to make a lot of these predictions.

So, let's see how some of this works, and hopefully your counterparts from 100 years ago would also be able to think about how this works, even if they don't have the quantum mechanics behind the individual electron configurations for atoms. So I said that we want to be talking about valence electrons here, so that means if we're talking about, for example, the octet rule for an f f molecule where we have two fluorine atoms, we need to write the valence electrons as dots around them. So let's do a quick clicker question, and you tell me how many valence electrons does fluorine have? Remember, valence electrons are different from core, they're only the outer-most electrons in the outer-most shell. So, 10 seconds on this, this should be fast.

OK, great. Good job on the clicker questions today. So we have seven valence electrons. So, let's go back to the notes, and let's fill these in, seven electrons. Another way you could have known them was to look at Lewis' notes here, where if look at this box carefully you see there are seven dots around the cube, so there are his seven valence electrons.

So, we see is when we use the octet rule to look at fluorine molecule, we're combining two fluorine atoms, and what we end up with is an f f molecule where they're sharing two electrons, so making that covalent bond. But that each individual fluorine atom has eight electrons, or full octet around it. We can think about where those electrons came from, so we got seven from the blue electrons here, seven as shown in green here, but each individual fluorine atom has eight, even though two of those are being shared between both of them.

So, the octet rule is a general rule that you'll for all of the atoms. There are some exceptions, which we'll get to later, but the only a big exception here is with hydrogen, which has a special stability that's associated with two electrons. This should make a lot of sense, because we know that a hydrogen has 1 s as it's outer-most or valence orbital, so it can be filled up just with two 1 s electrons. And we give different names, depending on what kind of electrons we're dealing with, so, for example, with h c l here, we can talk about having bonded versus lone pair electrons.

So, in terms of the c l atom, we need to talk about each atom individually. How many bonding electrons does c l have? All right. Let's see, we've got a mixed response here, it turns out it has two bonding electrons. I heard some people say one, and that's a good guess, remember they're actually sharing. So these two electrons, they belong to chlorine, they also belong to hydrogen, but they do, in fact, belong to chlorine as well. There's no one person owning them, so they both have two electrons here that are bonding. So how many lone pair electrons do we have?

OK. I hear six and three, so both are sort of right, we have 6 lone pair electrons, which means that we have three lone pairs. So, in terms of thinking about how to draw a Lewis structure, I won't go through this today or any day in terms of just reading through the rules, you can read that yourself. But what we'll do is go through each of these rules in terms of an example. So, what will start with on Monday is doing the most simple example of methane using these Lewis structure rules.

So, don't forget to study this weekend and get those extra practice problems from the course website.