Lecture 19: Biomimicking

• Download this transcript - PDF (English - US)

The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation or view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

LORNA GIBSON: All right, well, I guess I may as well start. I don't know if anybody else is going to come. So I wanted to finish up by talking a little bit about the biomimicking. And some of these examples, you've seen before. But I just thought I'd put them all together, and we could look at them as one thing.

So if you remember, when we talked about wood, one of the things that I showed you was that people have taken wood and pyrolized it. So they get a carbon template of the wood cells. And then they infiltrate that with silicon carbide-- or, with a silicon vapor infiltration. And they make a silicon carbide ceramic. So they can get a replica of the structure.

So sometimes when people say "biomimicking," some people think of it as replicating something. But it doesn't have to be just replicating something. It can be also just some design inspired by the biological material. But this thing really is a replica. And this was another version where there was the-- they took the silicon carbide material and then infiltrated that with liquid silicon to get a fiber-reinforced material, really. So there was the wood composites we talked about.

Jennifer Lewis's group up at Harvard is doing 3-D printing of honeycombs. And one of the things they've been interested in is not just printing of the pure resin, but having a fiber-reinforced resin. And the first thing they did was they made these honeycombs like this. And they had small silicon carbon fibers-- or, were they silicon carbide? Maybe it was carbon fibers-- in the ink. And so they would just-- if the ink was being laid down, the fibers would just line up in the direction of the ink. And so the fibers tended to be in the plane of the honeycomb.

And if you think of things like wood, you want the fibers to normal to that plane. And more recently, they've-- hello. Oh, hello. Oh, look. Oh, look, almost everybody is here. So more recently, they've got a technology now where they're rotating the nozzle as they print the honeycomb. And as they rotate the nozzle, they get some change in the orientation of the fiber.

So they're beginning to be able to make honeycombs that are fiber-reinforced. And they can get the fibers aligned with the prism axis of the honeycomb, which is more or less what the wood does. So I wasn't going to write anything on the board today. I was just going to go over some of the slides and do the review.

So they're beginning to make honeycombs that have the same sort of structure on the cell wall level, or at least a similar structure, as to what the wood composites have. So that's another example there. This is just another close-up of their fiber-reinforced walls in honeycomb specimens.

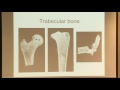
We talked about trabecular bone, and we talked about the fact that people are starting to look at using foamed metals as coatings on orthopedic implants. And there's been some interest in looking at using foamed metals for more permanent parts of the body, more permanent bone parts, things like vertebral cages, stuff like that. And so this is just an example here, with the trabecular bone on the left and the tantalum foam that's made by replicating an open-celled polyurethane foam on the right. And you can see the similarity in the structures of those two things there.

Then we talked about tissue engineering scaffolds. And if you remember, these two scaffolds here on the bottom were made from pig heart tissue. And they're made by just removing all the cells. So that actually is the natural extracellular matrix.

And then, these other structures up here, these were all engineered tissue engineering scaffolds that are made in a synthetic way. And the idea is to try to mimic the extracellular matrix in the body. So you can see the similarities there.

And then more recently, we were talking about sandwich panels. So this is the example from the helicopter rotor blade. That's from an aircraft flooring panel. And this was the Irish leaf, and these were the bird skulls. So the same sort of idea, that there's these engineering lightweight structures, and there's also similar things in nature.

And then, I think, last time, we also were talking about palms. And the palm stems had density gradients in them. And one of the things we showed was that by having that density gradient, the stress distribution across, say, the radius of the palm was almost matched by the strength distribution. So it was a very efficient way to use the material.

And at MIT, that was a student in architecture who was looking at doing this with concretes with aerated or foam concretes and making a radial density distribution. So he made beams. He made columns. He made different kinds of things. With the concrete, there's a little bit of a limitation, because the concrete is much stronger in compression than it is in tension. So if you had a beam loaded in tension or a concrete column that might buckle, you'd still have to have some reinforcing bars in there to take the tensile loads.

And one thing I think I didn't really talk about was animal quills and other sorts of plants stems. And many of these have a structure that's made up of a cylindrical shell with a foam or a honeycomb core. So here are some examples in nature. If you look at grass stems, there's a dense layer on the outside, and then a foamy layer on the inside, and then just a hollow layer in the middle.

And if you look at porcupine quills-- this is a porcupine quill-- these are made of keratin. They're like modified hairs. So it has a dense layer on the outside, and then this foamy stuff on the inside. This is a hedgehog spine here. And again, you can see there's a dense layer on the outside and these ribs on the inside.

And this is the toucan beak-- you know, the toucans that live in Central America. And the beak has a foam core. Again, they're keratin structures, and yet the outside is solid. But the inside has a foamy structure. And Mark Myers did a paper on this a while ago.

So we got interested in these structures that have a solid shell on the outside but a foamy thing on the inside. And we wondered if there was a mechanical reason for that. And you can show that, at least in some of them, if, say, you have a grass stem-- it's really common in plant stems. Do I have some more plant stems? Yeah, here we go. Here's a milkweed stem. So it's got these dense fibers with this foamy core here. And blue jay feathers-- feathers have this as well. So they have an outside layer on the quill that's solid, and then an inside layer that's foamy.

If you look at things like plant stems, they blow in the wind. And you can look at the buckling resistance of the stem. And because there's this shell with the foam-like core, it's not just the overall buckling of the whole thing. You can get that local face-wrinkling mode again. So the outer shell can wrinkle. And you can show that having a foam-like core helps prevent that wrinkling from happening, the same as with the sandwich panel.

You remember we talked about the face wrinkling on the sandwich panel? Well, on these stems, you can get wrinkling of the outer shell. And the foam helps prevent that from happening. And you can show that you can actually-- for the same buckling load, you can reduce the weight of the plant stem, or the bird feather quill, or whatever by having that foamy core.

So people have looked at this too. And there's a group in Germany who had looked at the idea of mimicking the horsetail stem. So this is a plant stem here, the horsetail plant. And they made something they called a technical plant stem, where they made this structure here.

And they made it out of fiber-reinforced composites. And you can see, the little holes here represent those holes there, in the plant stem. So the idea was to try to get something that was good at resisting the buckling, but at a lower weight. And they were doing that with this thing here.

And there was a group in Japan that did a similar thing. They used-- I think they took a copper tube, and then they took copper and aluminum wires and filled the copper tube with the wires. They extruded that. And then they melted out the aluminum, which, I think, also helped to soften and make the copper bond together. And they got these structures here. And you can see, that's similar to some of the plant stems as well.

So these are all examples of cellular structures that have-- mechanically efficient structures. They're lightweight, and they're strong, and they're stiff. And these natural structures have been mimicked in engineering applications. So that's really all I wanted to talk about today. But I think we wanted to use the rest of the class as a review.

So I haven't made a one-hour summary of the last six weeks, because that's not really possible. So I thought I would just answer questions. If you have questions, I'll try and answer them.

So for the test-- so, the test is on Wednesday. You can bring one 8 and 1/2 by 11 sheet. I wasn't going to give you all those honeycomb and foam equations, partly because-- the only thing I would really want you know is open-cell foams. And I was hoping, by now, that you might have registered those equations somewhere in your brain.

So I'm not going to ask you for-- some equations are obscure. I might ask you-- expect you to know what the Young's modulus of an open-celled foam is by now, or the axial modulus of a honeycomb or something. But I don't think I'm going to ask you anything like, calculate air pressure contributions to the modulus of the closed-cell foam. I don't think we're going to do that on this test.

So I think you should know what the modulus of a-- the Young's modulus of an open-celled foam is, the shear modulus of a foam, because you need that for the sandwich panels. But you don't need reams and reams of those equations, so I wasn't going to give you those this time. OK?

So Jenny, did you have-- so I finished the biomimicking thing. We're just going to do a review. I don't know if you want to stay or if you want to go. You want to stay? Well, whatever. So do you have questions, Jenny?

AUDIENCE: I do. I just wanted to have question 4 from the last pset reexplained. Because I know that you explained it to in office hours, and I know that the solutions are online, and I looked at them. I'm still confused.

LORNA GIBSON: OK. So, you're going to have to remind me what problem 4 is, because I don't remember.

AUDIENCE: Question 4 says, polymethacrylate foam at solid strength of 3.0-- or, solid Young's modulus, rather, of 3.0-- gigapascals is being considered for the energy absorption layer in a bicycle helmet.

LORNA GIBSON: OK. I'll tell you what, I think I have it on my little disk here. Maybe that's easier, because then I can read it.

AUDIENCE: [INAUDIBLE].

LORNA GIBSON: Yeah, let me just see if that's going to come up. There it is. OK. So this one here about the foam, about the--

AUDIENCE: The one with the graphs.

LORNA GIBSON: --energy absorption?

AUDIENCE: I'm just a little bit confused by the graphs.

LORNA GIBSON: OK. Let me see if I can make this bigger. Hang on a sec, my computer's thinking. OK. OK. And I think I gave you-- right, I gave you this graph here. Right?

AUDIENCE: Yes.

LORNA GIBSON: OK. So can you read what I've got here, or is that-- should I make it bigger?

AUDIENCE: I can't really read it, [INAUDIBLE].

LORNA GIBSON: Does that help? OK. So I have to admit, when I put this together, somebody-- I can't remember who it was-- told me you thought it was overconstrained. And it turned out it was overconstrained. And then I said, forget the thickness. Forget that I've given you the thickness, right? So disregard the thickness.

AUDIENCE: No, the velocity.

LORNA GIBSON: Oh, speed-- the speed? The speed-- all right, OK, the speed. No, I don't want to register. OK.

So from what I gave you, you can figure out the normalized peak stress, right? So you can get-- so if I do this, is this good? You can see what I'm pointing at? So you can get, the peak stress is just the mass times the acceleration over the area-- are we good with that-- divided by Es, which I gave you. So I think most people probably got the peak stress here.

And then, because I had given you the velocity and the thickness, I was thinking you could calculate the strain rate. But if I don't give you the velocity, say we're not calculating the strain rate at this point here, OK? So here, we're-- did I put this-- I don't know if I have the graph on this solution. There we go.

So this point here is the 2.5 times 10 to the minus 4 for the peak stress. And if you're not given the velocity, I think what I thought you would do then would be just assume a velocity. And then you can check it at the end. So since I had given you this velocity of 12, let's just say that's what we assumed. OK? So then you get a strain rate of 480 per second. So let's just say we assumed that velocity.

Then we could scoot back over here. So we know we're on this line here for the sigma p over Es. And we want to be up towards the top of these different strain rates. So if you look at the strain rates, see, the very last one at the top is 1,000 per second, and the next one's 100 per second. So we're halfway in between those. And they're so close together, you can't really read the difference. But we're up here somewhere. So then we read off a w over Es for that. OK? Are we good?

Then, if we know the w over Es, this is the number, here, that I read off. You know what the Es is, so you can get w. If you can get w, w is in joules per cubic meter. It's in energy per unit volume. But you know the area, and you know the thickness. So you can get the energy in joules.

And then-- oh, did I-- I must have rubbed that off. Didn't have it on this version. The version in my notebook, I think, calculated what the velocity would be that corresponds to this. And I think it turned out to be 8 meters per second or something. So I had assumed 12, and I think it worked out to 8. And on those log log graphs, whether or not it's a strain rate of 480, or a little bit less, or a little bit more, you can't read the difference on these things. OK?

AUDIENCE: Can you explain how this graph relates to the other graphs from lecture that were simpler? Because we had ones that were all density, and ones that were all the same strain rate. And I guess I'm just confused why.

LORNA GIBSON: Oh, OK. Hang on. So let me see if I can-- hang on. No, I think I know what you mean. Let me see. I want to pull up the lecture notes. I think I'm finding the right thing. Here we are.

So in the lecture notes, there was a thing that looked like this. Is that what you're talking about? Yeah. So the top set are the stress strain curves. So those are OK. You do a compression test, you measure that.

Then, the middle set, you take, say, for one density, for one stress strain curve-- say that's your curve, the middle one there, 0.03. Say you loaded it up to some point, or say you looked at some point here, on the curve. You would figure out, for that stress, what's the area under the curve up to that stress. So you'd have a stress and an area under the curve up to that stress.

And you could then-- say we know what this foam is. It's-- I don't know-- a polyurethane or something. So say we know Es. Then we could divide those two numbers by Es. And we would plot that one thing. Let me just walk over here. So this is the 0.03. So if it's in the linear elastic reading, it would be somewhere in here.

Then I would scoot along, say, to here someplace. I would do a whole bunch of points all the way along there. And at every point, I would say, what's the stress, and what's the energy absorbed up to that stress. OK? And then I would plot-- doot, doot, doot, doot, doot-- up here, I would plot all those points. OK? And then when I got to this part here, that corresponds to that part over there. OK? Are we all good with that?

OK. So then we repeat-- so we get one curve on the middle chart. Then, for the different densities and the different stress strain curves, we plot a different curve for each of the different densities doing the same process. And the thing we notice is that these points here are really the optimum point. Because at that point there, you absorb as much energy as you possibly can for that stress. OK?

And we notice, happily, that those points lie on a line, basically, on a straight line. And we tick of what the different densities are-- so 0.01, 0.03, 0.1, 0.3. OK? And that line there, and all of these stress strain curves, and all these lines here, curves here, they all correspond to one strain rate. All right?

So now I could take that line there for that first strain rate, and it would be one of these thinner lines here for a particular strain rate. And I would mark off-- just the same as I've got here, 0.01, 0.03-- I'd go 0.01, 0.03, 0.1, 0.3. All right? And then I would repeat this whole process again for a different strain rate.

So I'd go back to doing some mechanical tests at, now, a new strain rate. And typically, the new strain rate is going to be bigger or smaller by a factor of 10 or so, because you're not going to see much difference in the behavior unless you get big changes in the strain rate. So you're going to change the strain rate significantly.

You get a new series of these stress strain curves. Then you get a similar-- very similar, but not quite the same-- series of these curves here. And what you'd find is you'd have another line here that would be offset a little from the first one. And the positions of where these densities were would also be offset a little from the first one.

And then you'd draw the second one. So the second strain rate line would go here. And the little density positions would be offset a little bit, and you would mark them off. And you basically repeat it for different strain rates, and then you build this thing up. And then the density lines connect too. Is that OK? So that's how you generate that. So the idea is, this bottom diagram is really summarizing all of those shoulder points. The bottom diagram is really summarizing all of these points where the stress starts to scoot up at the densification machine.

Yeah?

AUDIENCE: So in question 3, we were constructing the graph in the middle for this particular one. What confused me is that on the graph, the variable on the x-axis is stress, whereas in the question, we were given the stress. So I drew something that looked as it should have looked. And it turned out to be right, but I'm very confused as to why.

LORNA GIBSON: OK. Let me try and get rid of that. And I'm going to have to remind myself what the question is again. OK. So we have an open filled aluminum foam. I asked you to write the equations for each of the different regimes. And those were straight out of the notes, I think. Right?

AUDIENCE: Yeah, I think the three inputs were different relative densities.

LORNA GIBSON: Yeah, and then you had to construct the energy absorption curve based on those equations. And I give you three relative densities. So this was my solution. So all this stuff here, I think, was straight out of the notes. So there was the-- oops, let me back up so we start at the beginning.

So there was the linear elastic part. There was the stress plateau. That was just as it starts to densify. And then, there's that line joining up the points. So you were OK with all of that?

AUDIENCE: Yeah. No, the only part that confused me is because once I simplified-- I inputted all of what we were given such that I had equations in terms of the relative density so I could just apply it to the different ones given. But then I wasn't very sure how-- because I got constants, I wasn't really sure how-- the slopes should look like, because they were constants.

LORNA GIBSON: So you got-- I'm not sure what you mean about you got constants. So what I did was I said, well, I know that the diagram has to have this basic shape, right? In the first part here is where it's linear elastic. And this part here is the stress plateau. And that part there is the densification. OK? And I said, well, if I can find these two points that correspond to the change between the linear elastic part and the stress plateau and the point that corresponds to the stress plateau and the densification, then I've got the diagram. Right? OK?

AUDIENCE: Yeah, I think that--

LORNA GIBSON: Oh, can I stop talking now?

AUDIENCE: I mean, if you wanted to--

LORNA GIBSON: Well, it's for you. So you're OK?

AUDIENCE: I think.

LORNA GIBSON: You.

AUDIENCE: So what confused me about this question was that in order to find the two points, you'd need to know the strain at which that [INAUDIBLE]. So I wasn't sure how you would find that strain.

LORNA GIBSON: Yeah, I think I didn't tell you. Let's see. Well, let's see. Do you have to have the strain? You have that. I think if you have-- I think you don't have to have it in terms of the strain. I suppose you could put it in terms of the strain. I mean, that would be a different way to do it.

AUDIENCE: But isn't the equation for the stress plateau already in terms of the strain?

LORNA GIBSON: Yeah, but this assumes that the stress plateau is just perfectly flat, right? So this thing here would be useful, the strain at which the plateau starts. But I think that's the same as saying-- that's the same point as saying you're at that point there, because that's where the plateau starts. OK? So I think there's different ways you could try to approach this.

But I think-- let's see, I'm just trying to remember what I did here. Yeah, so what I did here-- so to get point a, I said, well, this is the equation for the linear elastic bit, right? And this is the equation for the stress plateau. Where I'm at point a here, this stress is the stress plateau. So that's why I've put sigma star plastic there.

And then I said, this is-- the sigma star plastic is-- and this works out to some number here, some number times the relative density to the 3/2 power. And then I just made this little table here, where I said, OK, these are the densities I need to get the curve for. This is going to be my sigma star plastic for those densities. And from that, then I can get this column here. It's basically just that equation with this substituted in. And do you see that that corresponds to the point a?

So I mean, you could do it by figuring out what that strain is and then figuring out all the points along that line up to that strain. But you don't have to do it that way. Do you know what I'm saying?

So you're saying-- if I had-- so say I have my idealized stress strain curve like that, right? You're saying, well, I had to know that strain there so that I know where this stops, right? And I'm saying that corres-- and you could do it this way if you wanted to. You could say that this is the energy absorbed up to that point. And if you know that the modulus goes as the relative density squared times Es, and you know this, if you know those two things, you can figure out what that strain is. So you could do it that way if you wanted to, but I just did it a slightly different way.

AUDIENCE: Yeah, so I don't understand how you just were able to get rid of the epsilon minus epsilon on that curve.

LORNA GIBSON: Oh, let's see. So I think, in the first part, where it's linear elastic, I just go up to epsilon 0, right? So this part here doesn't really involve the epsilon, because I've gotten rid of it by taking the square of the stress. And then here, the other point I'm looking at is this point here. And I've assumed that epsilon 0 is much smaller than epsilon d, and I've ignored it. And that's, I think, how I did it in the notes in the class. OK?

So when you get to that point, this strain here is usually a few percent at most. And this strain here is typically 80% or 90%. So it's pretty common to do that. OK? Other questions?

So don't forget, the test covers everything from the thermal conductivity of the foams, it covers the stuff on trabecular bone, sandwich panels, and then, the energy absorption stuff. Yeah? Are you a little exhausted already? Yeah. So I'm guessing that this week and next week, you have everything due. You have papers, and projects, and tests. Do you have very many exams left, like final exams? Yeah, you've got finals?

AUDIENCE: [INAUDIBLE].

LORNA GIBSON: Oh. All right. Anybody else have any questions? Because I think we can just go and do other things if nobody has any other questions. So the test is on-- so let's just review where we're at for the rest of the term.

So the test's on Wednesday. And you can bring one cheat sheet, but I am not giving you all those equations with honey combs and foams. So I think, on your cheat sheet, you would want to put Young's modulus of an open-celled foam, shear modulus of an open-celled foam, compressive strength of an open-celled foam, shear strength of an open-celled foam. But I don't think there's going to be anything more complicated than that.

And Monday, I was going to do the how I became a professor talk. So if you've seen it and you don't want to see it again, you're welcome to not come. But for you guys, I just talk about how I got here. And it's about my life. It's not about cellular solids or anything. And I don't know, you guys liked it. You like it, don't you?

AUDIENCE: Yeah.

LORNA GIBSON: Yeah. Yeah. So if you want to come, I'll do that. And then Wednesday, I thought, I just need to collect the projects. I wasn't going to do anything on Wednesday. And so I've been thinking about the how I became a professor talk. And I think-- so I have this idea that students would like to hear more of these talks from other faculty. Would that be true?

AUDIENCE: Yes.

LORNA GIBSON: Ah. Because I've been in touch with Cindy Barnhart, and we're going to try and organize something for the fall. So I'm going to approach some other professors-- not just in our department, across all of MIT-- and see if I can get other people to do the how I became a professor talk. So you would like that? OK, yeah. So we'll see if we can make that happen.

Free Downloads

Video

• iTunes U (MP4 - 68MB)
• Internet Archive (MP4 - 68MB)

Subtitle

• English - US (SRT)