Lecture 18: Natural Sandwich Structures; Density Gradients

• Download this transcript - PDF (English - US)

The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high-quality educational resources for free. To make a donation or view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

PROFESSOR: All right, then, I guess we may as well start. So what I wanted to talk about today was natural sandwich panels and sandwich beams. So there's lots of examples of sandwich structures in nature, and we've been looking at the engineering sandwich structures. And we've seen that you can get a lightweight structure by having this sandwich construction. And so there are several examples I was going to talk about today. And I think because this isn't really on the test, I'm not going to write a lot on the board.

So there's some notes. I'll just put them on the website, and you can look at that if you want. Because we have kind of a shorter time today. I'll just try and talk and explain what's what. Hey, Bruno. How are you?

So this is the first example. So many leaves of Monocotyledon plants have a sandwich structure. And this is an iris plant and iris leaves. And for those of you in 3032, I think you know that these are glass flowers.

So the Harvard Museum of Natural History has a glass flower collection that was made in the 1800s. And there was a botany professor there who made these as sort of a lecture demonstration vehicle. And so he would bring then to class, and he would show different things about the plants with the glass flowers. But now they're just in the museum, and they're very realistic. So I just wanted to show you those.

So let's see, it's not working. Turn it on. There we go. So if we look at a cross-section of an iris leaf, it looks like the diagram on the left. So here's the iris. And you can see there's these kind of solid fibers, and those solid fibers are called schlerchyma. And they only exist at the top and the bottom of the leaf.

So I went out this morning. And if you look outside of the Stata building, there's that little kind of river-y thing, and there's some iris leaves growing there. So I went and got some iris leaves. And you can tell we had a horrible winter because usually when I give this lecture in the spring, the leaves are like twice as big. But this year, they're just little, short, wimpy ones.

But I'm going to pass it around. And if you just like move your thumb over the top, you can feel little ridges, little bumps. And those little ridges that you can feel are these little schlerchyma fibers. So you kind of see they kind of stick up a little. And so when you move your thumb over it, you can feel that. And then you can see that the middle of the iris leaf has this kind of foamy-type structure here, and that's called parenchyma cells.

So you can think of the leaf as very much like one of the sandwiches. This is like a fiber-reinforced composite at the top and at the bottom. And then this is kind of like a foam core in between, separating the fiber-reinforced faces. And so the iris leaf behaves mechanically like a sandwich beam. So I'm going to talk a little bit about how we can actually demonstrate that using the equations that we developed in class.

This is another example. This is, I guess, what Americans call the cat tail, but Canadians and English people call it a bull rush. And you can see this is a slightly different construction, but there's the same sort of idea. So instead of having a foamy core as in the iris leaf, you've got these kind of webs here that go in between the top and the bottom, and that forms like a series of I-beams almost. And you can think of that also like a sandwich panel or a sandwich beam.

So you've got two stiff top and bottom pieces, and then you've got these kind of webs that separate them, kind of like a honeycomb core would be. So that's another example of a leaf that has the sandwich-type structure. And this is very common in these Monocotyledon leaves.

So if you think of a cat tail or you think of an iris, they tend to be kind of narrow at the base, maybe an inch or two wide at the base, and they can be quite tall. The iris leaves can get two or three feet tall. The cat tails can get five or six feet tall. And they stand up more or less straight.

They bend over a little, but they stand up more or less straight. And this sandwich structure is one of the things that lets them stand up straight at a fairly low weight. And from the plant's point of view, there's a sort of metabolic cost associated with making more material. So it we can minimize the amount of material, it's a better thing for the plant.

These are some other examples of grasses that are sandwich-type constructions. This is from some papers by Julian Vincent. And the black little circles here are the schlerchyma, are those sort of dense fibers. Then you can see in both of these cases, the dense fibers are on the outside, and the parenchyma cells, which is the white, are on the inside. And so this is sort of another set of micrographs of the iris.

So this is just showing the outside, and these are the ribs viewed from the outside. And this is the core, just sort of viewed along the length of it. And so you can idealize the structure as being like a sandwich that's got sort of fibers on the top and on the bottom. So the top and the bottom are like a fiber composite. And the middle part, with the parenchyma cells, is kind of like a foam. And so we did a little project on iris leaves, and we wanted to see if you could show that they behave mechanically, like a sandwich beam.

So you remember that we had that equation for the deflection of the sandwich beam. There were two terms. There was a bending term, and then there was a shearing term. And so we took some little sandwich beams. We cut little kind of rectangular beams. We hung little weights. We measured how much they deflected, and we wanted to see if we could use this equation to predict their stiffness and how much they deflected.

So to do that, we needed to know a bunch of things. We needed to know some of the geometrical parameters. So we needed to know what volume fraction of the face is those solid ribs, how thick's the core, how thick's the face? And so we measured a bunch of these geometrical parameters. We tested it like a cantilever so we knew what B1 and B2 were for the cantilever. We knew how long the beam was, so we know what l is. We knew what loads we applied, so we knew what P was.

But we needed to make some estimate of what the face modulus was and what the core shear modulus was, too. And so we made some estimates of that. So this table here just shows some of the dimensions of the leaf. The leaf tapers, and this is at the thin end, so here's the face thickness.

Here's the sort of length of this. Some square cells in the face. This is the core thickness here. This is the dimensions of the core cells. This is the diameter of the ribs, the spacing of the ribs, the volume fraction of solids in the ribs. And we did that at different lengths along the different positions along the length of the rib, or length of the leaf.

So we had the geometrical parameters, but we needed to get this E of the face and G of the core. And to do that, we looked at the literature. And people had done tests on the fiber parts of leaves. They'd done little tensile tests, and they'd measured modulii between about two and 20 gigapascals. And then we did some tension tests on the iris leaf. And in tension, those ribs are going to take most of the stress. And if you know the volume fraction of the ribs, you can back out what the stiffness of the ribs must have been.

If you know the stiffness of the ribs, you can figure out the stiffness of the face. So we calculated that, and then we looked at the literature. And people have done tests on parenchyma cells and different types of tissue on things like apples and potatoes and carrots. And these are the values for the Young's modulus they get. They're between about 1, and the highest one was 14 megapascals.

But most of these values for the Young's modulus are around about four. And the shear modulus is roughly about half of the Young's modulus. So we said the shear modulus was around two. So we have these values we could plug it in and then calculate what the stiffness would be for the iris leaf. And so this was a little analysis we did.

So this was the measured beam stiffness up here. We had four beams, and they were different stiffnesses. They all had the same length. They all the same face thickness. The core thickness varied. They all had the same width. We cut them to have the same width so we could calculate a flexural rigidity. That's the EI equivalent. We could calculate the bending deflection term, the shear deflection term. And this is the calculated beam stiffness. And then this is the ratio of the calculated over the measured.

So it's not exactly right. Obviously, there's some difference here. But it's in the same order of magnitude. It's in the same ballpark. And one of the complications that we didn't really try to take into account was that the leaf isn't a nice rectangular structure. The leaf has this kind of curved cross-section to it. And we made a bit of an approximation to that, but it wasn't that close, really. We could have probably done better on that.

But I think the idea that the iris behaves like a sandwich is a reasonable one. So that was the iris leaf. And then I wanted to show you some other structures in nature that are sandwiches. So this is a seakelp, help like a seaweed thing, in New Zealand. This is the largest intertidal seaweed.

The fronds, the sort of long pieces of it, are up to 12 meters long. So that's almost 40 feet. So 40 feet is probably like from one side of this room to the other side of the room. It's quite long. And you can see, if you look at this section here, this is all like a honeycomb-type section here. And the honeycomb is like a honeycomb in a sandwich, and the top and the bottom faces are like the face of the sandwich.

So this would be like the face here. That would be the honeycomb core. And that would be the other face on the other side over there. And those honeycomb-like cores, apparently, have some gas-filled pockets that then provide buoyancy to keep the whole thing floating. So it photosynthesizes.

So one of the things about these leaves is that they have multiple functions. It's not just that they have to have a certain stiffness so they don't fall over. The plant wants to photosynthesize, so you want to maximize the surface area as well, and you want to have exposure to the sunlight. So there's a number of things that the plant's trying to do in having this structure.

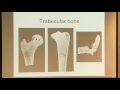
So that seakelp is one example. These are skulls from birds. And so this is a pigeon here. This is a magpie. If you come from the West you see magpies out West. You see them in Europe as well. And this is a long-eared owl. This long-eared owl's around here. And I brought in a couple of bird skulls as well. And you can see that all of those birds skulls are sandwich structures.

The one for the pigeon has sort of a foam-like core here. And you can see that the two faces aren't sort of concentric for the pigeon skull. They sort of not following each other. But here, this would be, say, on the top shell of the magpie, where the two, the inner and outer face, are sort of concentric.

Then you get these kind of little ribs of trabecular bone in between them, and then the same with a long-eared owl. You get these little ribs in between them. And so you can see that there's a sandwich structure there. And obviously, birds want to be light. They have to be light to fly, to take off, and so they want to be light.

So I've got two skulls here. And I'll pass them around. Please be careful because they're kind of delicate. This one is from a screech owl, and you see screech owls around here. This was a screech owl that had an intersection with a car. Yeah, so the skull fractured, but you can see the sandwich right there. You see the two little bits? So you can see the inner plate and the outer plate and the foam, the trabecular bone.

So that's the screech owl. And this is a red tail hawk. So you can't really see the shell and the sandwich structure here. But I want to pass it around just so you can see how light it is. So it's amazingly light. So a red tail hawk is probably about this big, something like that. And this is one of the things that makes them very light.

So those are the bird skulls. Oh, yes, so now I have to tell you about the owl. So I think the people in 3032 have heard this before. But the other people haven't. So one of the things about the owl is if you look at the whole skull, if you look at this picture here, one of the things is that this bone here is not symmetrical with that bone there.

Normally, when you think of a body, you think of the bones being symmetrical. But those bones are not symmetrical, and those bones are near where the ear is. And it turns out on owls, at least on some owls, the ears are at different heights on their heads. And people think that one of the things that allows the owls to do is it allows their hearing to sort of pinpoint where something is. And owls can catch little creatures at night, but they can also catch little creatures underneath the snow.

So they can catch things that they can't even see. And they have a number of adaptations to improve their hearing, but this is one of them. So here's a little owl Allison Curtis is a Canadian friend who lives in northern Ontario, and this is looking out of her living room window. And that's a barred owl. And you can see the barred owl has caught this little vole here. And you can see in the background it's winter in Canada. and there's snow all over the place.

So this owl has probably caught that little vole underneath the snow. And then it's come to eat it. And this is another picture of-- you can see this is where an owl landed in the snow. It's wings hit the snow, trying to catch something underneath. And this is another kind of beautiful print of the owl's wings hitting the snow in the winter time.

So did I show you the fox video? Should I show you the fox video? You saw it, right? I think I showed it last time in 3032. But you guys haven't seen it. Let me show you the fox video because foxes do the same kind of thing. Their ears are the same as ours. They're in the same position. But they have this-- let me see.

Where's the sound thing? We don't really need the sound for this, but there's BBC sound. So we get this music, even though the fox can't hear the music. Here we go, fox no drive. Check this out. Is it going to come up? Is that going to play? OK

[VIDEO PLAYBACK]

-It listens for the tiny sounds of its prey moving about below.

PROFESSOR: So you see how it cocks its head, and it does this with its head? It's putting its ears at different heights when it does that. So check this out. And look carefully, you can see the little animal it's got in its mouth when it comes out. There's a little tail. So part of the reason dogs and foxes and coyotes do that thing, I think, is because they put their ears at different heights, and it helps them pinpoint where something is.

[END PLAYBACK]

You know I love these Nature videos, right? So that's the fox video. Let me see if I can stop that. So that's one of the interesting things about owls. Let me go back to my little PowerPoints.

So here's another example of a creature that has a sandwich-type structures. So here's the sandwich here. Here is the ever so charming looking cuttlefish. And the cuttlefish is not actually a fish. It's a mollusk. So it's related to things like octopus, things like that, and squids. It's a cephalopod. And you can't see it so well in this picture, but I'm going to show you something else and you see it.

It's got like little tentacles. These things here are actually separate little tentacles. And because it's not a fish, it doesn't have like fins that can kind of swim with. And it's got this thing called the cuttlefish bone. And this is a cuttlefish bone here. And that bone has the sandwich structure here. And it's not actually a bone. It's really a shell. It's a calcium carbonate thing, not a calcium phosphate thing.

But the cuttlefish can control how much air goes into those little pockets. And it can control its buoyancy by controlling how much air goes into those little pockets. And I brought with me a cuttlefish bone. Have you ever owned like, I don't know, like a parrot or a pet bird? Apparently, pet birds love to sharpen their beaks on this cuttlefish bone. So if you go to a pet store, you can buy this stuff.

So you won't be able to see the little sandwich structure because it's a very small length scale. But you can kind of see there's a sort of different material on the inside than there is on the outside of that. So do people know the other thing that cuttlefish are famous for, besides the bone? Change colors. Can I show you a video of cuttlefish changing color? Yeah, of course.

So let me get rid of this again. Go back to this. Let's see, somewhere-- where's the cuttlefish? Here we go. Did I do it? Is it thinking? Here we go. Where's the cuttlefish? So this is another one of these Science Friday videos from National Public Radio with Flora Lichtman.

[VIDEO PLAYBACK]

-OK, let's play a game.

[GAME SHOW MUSIC PLAYING]

[APPLAUSE]

PROFESSOR: See it?

-Biologist Sarah Zielinski took these shots. And if you needed a helping hand to find the cuttlefish, don't feel bad.

-I've certainly taken photos in the past then come back to look at them and gone, I'm sure there was a cuttlefish in there somewhere!

-These cephalopods are master camouflagers. But while they're hiding their body, they're revealing something about their mind, or at least their visual system.

-In very simple terms, they can tell us what they can see by the body patterns they produce on their skin.

-They produce these body patterns by expanding or contracting chromatophores, these little ink sacks on their skin. And they use different displays for different reasons, like for male-to-male combat.

-Two males will turn into each other and pass these kind of waves of dark chromatophores over a really bright sort of iridescent stripey body pattern and somehow solve these combats. Eventually, one male gives up and goes away.

-And then there's this unsolved mystery. It changes color when it grabs a snack.

-That doesn't make perfect sense because it seems to make it very conspicuous. So one theory is that it's just a happy signal of how excited it is to have caught something, some response that it doesn't have any control over.

-But most of the time they seem to be using their chromatophores more intentionally, primarily to blend in.

-Because otherwise they're more likely to be eaten, so it's very important they don't make mistakes about ambiguous visual information.

-And ambiguous visual information is specifically what Zielinski's interested in. So here's the experimental setup. Print out laminated patterns, like this checkerboard, and stick them in a tank.

-And we place the animals in the tank. And we record the body patterns that they produce.

-You're seeing them on squares, but they do the same thing on top of circles. They produce--

- --the disruptive pattern, where you get these blocky components of high-contrast components.

-But when you put a cuttlefish over squiggles, it produces--

- --a sort of mottley pattern, where you get these little groups of dark spots showing across the body.

-So what happens when you put a cuttlefish on something in between, when you put them on incomplete circles? When we see something like this, our visual system likes to fill in the blanks, something we do constantly, Zielinski says.

-The reason why cartoons and sketches work is because we can recognize objects based on their edges alone.

-And we can identify objects even if they're broken up or--

- --have an object that is occluded by another object. That's no problem for us. We can still work out what the object is most of the time. And I was interested to know whether cuttlefish can solve similar problems.

-And Zielinski and colleagues report this week that cuttlefish do seem to--

- --fill in those gaps and interpret those little segments as a whole circle.

-Or anyway, the broken circles prompted the same camo pattern as full circles. So if you're wondering, uh, I see these as circles, too. What's the big deal? The weird thing here is that there's no reason why cuttlefish, which are--

- --invertebrates, and they're in the same group as slugs and snails.

- --should see the world the way we do.

-Yes, it's like they're alien, but we also seem to have so much in common with them.

-So the next step?

-Because we can't share the perceptive experience of a cuttlefish, it's hard to know exactly what it is that they're doing to fill in that missing information. And I want to try to get a better grasp on that and also see whether they actually respond to true illusory contours.

-So you're going to show optical illusions to cuttlefish?

-(LAUGHING) That's what I'm hoping to do, yes.

[END PLAYBACK]

PROFESSOR: So let's go back to sandwiches. I think I have-- do I have one more? There we go. So horseshoe crab shells, so different sorts of arthropods, the shells are sandwiched too. This is from Mark Myers' work. So we're looking at the cross-section of a horseshoe crab shell.

So again, it's the same idea-- the animal wants to minimize the amount of material or minimize the weight, and this is a way of doing that. And I went to the Galapagos about a year ago. And there was a place where they had these giant Galapagos tortoise shells. And one of them was broken, and you could see there was a sandwich structure in the Galapagos tortoise shells. These Galapagos tortoises, their shell is like this big. They're gigantic. They're huge.

So those are my examples of sandwich panels and beams and shells and whatnot in nature. So the idea is that nature too wants to minimize weight and minimize the amount of material, and the sandwich structure is a way of doing that. So I have one more thing I wanted to talk about today.

So this isn't quite sandwich structures, but it's looking at another kind of natural structure that is designed to reduce the weight of plant stems, in this case, palm stems. And there's a couple of interesting things about this. So when you look at palms, like let's pretend we're not in Boston. We're in California, where they have palms. And we're in LA, and they don't have winter. And if you look at the palms growing, when the palm's short, it's about this big in diameter. And as it gets taller and taller, the diameter doesn't really change.

It gets taller and taller and taller, but the diameter doesn't change, at least in some species. Whereas if you think of a tree, a tree starts out with a little skinny diameter. And as the tree gets taller, the diameter gets bigger. And it sort of tapers and does that whole thing.

So palms don't do that. And palms are not trees. They're a botanically different thing from trees. So here's a coconut palm. And so the question is, as the stem gets taller and taller, how does it resist the bending loads that get bigger and bigger?

So probably, the main load on these sorts of things is from the wind. And often these plants are in areas where they have hurricanes. And you see them in hurricanes, you see the pictures of the palm stem blowing way over. And so how do they resist the larger internal stresses as they get taller and taller, if the diameter doesn't get bigger and bigger? And the way they do that is that they deposit additional layers of cell wall as the plant ages.

So if you think of a tree, when a tree grows, it just deposits more and more cells. And the cells have roughly the same thickness. So there's ones that are deposited in the spring have thinner walls. Then the summer and the fall have thicker walls. But more or less, it's similar. Whereas the palm, it deposit cells, and then as the trunk of the palm gets taller, as the stem gets taller, it deposits more layers on the cell wall.

So this is an example in an SCM. You can see here this is a young cell, and it's got-- this one that's not marked is a primary cell wall, and then this is the first layer of the secondary cell wall. And then this is an older palm. And you can see here it's got more layers, and so the cell wall itself has gotten thicker.

So that means that the density of the tissue changes as the palm ages. And it does so in a very kind of clever way. If you think of the palm as being like a cantilever that's vertical and it's bending in the wind, when we have a cantilever beam or any kind of beam, the stresses are going to be biggest on the periphery, right? They're going to be biggest on the outside. And if you think of the palm as having a circular cross-section, that outer periphery is going to see the biggest stresses.

So it would make the most sense if that was the densest tissue. And that's exactly what the palm does. So there was a nice study done by Paul Rich quite a number of years ago. And he studied palms in Central America and looked at the density and measured the mechanical properties. And I'm going to talk about his stuff today.

So the white is the low density. The gray's the medium, and the black's the high. So you can see the low density's on the middle of the young stem, and just at the very base and then the periphery is the dense tissue. But as the stem gets taller and gets older, then stuff that was low density is now high density. And only the very middle here is the low density. And that some stuff that was low density has turned to middle density. And some stuff that was low density has turned to high density.

So it's done this by adding more and more layers to the cell wall, making the cell wall thicker and making the cells themselves denser. So this is looking just at a single palm. So each one of these lines is a single palm. And this is looking at how the density changes from the periphery to the center of the palm.

So if you cut the palm down and, say, we take a little sample radially from the middle to the outside or from the outside to the middle, he then measured the density. And it's probably easiest to think about the dry ones because that's kind of what you would compare wood to. So the dry densities varied from about one gram per CC, that's about 1,000 kilograms per cubic meter, down to almost zero in this particular species here, probably like 50 or something like that. And if you compare this with woods, this little arrow here is the density of most common woods.

So if you looked at pine and spruce an oak and maple and ash and hickory, they would all be in that little range there. So a single palm stem can have a bigger range of densities than many different species of wood. So it has this kind of profile of the density. And the thing I was interested in is seeing how mechanically efficient that was to put the denser material at the outside.

So I looked at the stiffness of the palm, and I also looked at the strength. So I just replotted that data on this slightly different axes here. So this is the radial position relative to the outer radius, and this is the density. And I subtracted off the minimum and then took the range. And for this species here, the minimum density was almost zero. So this expression simplifies to something like that. And just because it's mathematically simpler, that's what we're going to look at.

So the density goes roughly as the radius squared. And Paul Rich also did a lot of mechanical tests on the palm, and he took out little beams of different densities. And he measured the stiffness and the strength of the beams. So he measured the modulus of elasticity here versus density. And he measured the modulus of rupture here. And these are all along the grain. And he found that the Young's modulus varied with the density to the 2.5 power, and the strength varied as the density squared. And if the--

[BUZZING SOUND]

Oh, hello.

[LAUGHTER]

So these were just sorts of empirical findings that he made. If you have prismatic cells and you deform them axially, and the cell wall was the same in the different specimens, then the solid modulus would be a constant. And you would expect that the modulus of the beam would go just linearly with the density, sort of like a honeycomb loaded [? at a ?] plane.

But what he measured was that the modulus and the strength varied with some power of the density. And the reason for that really was that the cell walls of the denser material had more layers. And in the additional layers, the cellulose microfibular angle was probably different, so that the different layers had different stiffnesses. And if you have layers of differences, then you're going to get this power relationship.

So what I then did was I took his data, and I tried to see how efficient that would be in bending. So he had found that the density varied with the radius raised to some power. This power n was 2, but I wanted to do it just for a general case, so I said I was just n. And he said that he found that the modulus varied with the density raised to some other power m. And for him, m was 2 and 1/2. And so I could write just another equation saying that the modulus goes as the radius to the mn power. And then you could do a little calculation where you work out with the equivalent flexural rigidity is.

So you have to integrate up. You kind of say you have a little band at a certain radius. That radius has a certain modulus. And you can figure out the moment of inertia that goes with that particular radius. And then if you integrate it up over the whole thing, you can say that the flexural rigidity for the gradient density is some constant times pi times the outer radius to the fourth power divided by those two powers mn plus 4.

So m was the power here for the modulus. And n was the power there for the density. And then you could compare that with having the same mass just uniformly distributed over the whole cross-section. And then if you take the ratio of the flexural rigidity for the density gradient versus the flexural rigidity for the uniform density, you can show that it's this equation here. And then if you plug in these measured values for those exponents for n and m, you find that the flexural rigidity with the gradient density relative to the uniform density is a factor of 2 and 1/2.

So the stem is 2 and 1/2 times stiffer by having that density profile. So there's a huge sort of mechanical advantage to doing that. And just sort of physically, if you know the stresses our biggest on the outside, it would make sense to put the denser material on the outside. And then the other thing I looked at was the strength of the palm.

So imagine this is our very schematic palm here, and then there's a circular cross section. So I wanted to compare the bending stress distribution with the bending strength distribution. So the stress goes as the modulus times the strain, just Hooke's law. And here we're assuming that plane sections remain plane, like that's the standard assumption of bending.

So if you assume plane sections remain plane, then the strain goes with the curvature times the distance y from the neutral axis, the distance from the middle. So this distance here would be the dis-- [? same ?] at loaded with a loaded p here. That distance would be y there. And then I can plug in some things here.

So instead of E, I'm going to plug-in my relationship with the radius to that mn power. And here's my curvature, and instead of y, if I say that some radius, I'm going to say y is our r cos theta. And so I'm going to say that the stress goes--

[SNEEZE]

Bless you. Goes as radius raised to some power mn plus 1. And again, for the species I know what n and m are, so the stress goes as the radius to the sixth power. And then I can also compare with what Paul Rich had found for the strength. He found that the strength-- so sigma star is the strength-- was proportional to the density raised to some power q, and that power was 2 in the measurements that he made. And so I can say that the strength goes as the radius to this power nq, so to the fourth power. And then if I plot the stress distribution and the strength distribution-- so imagine, this is through the cross-section here.

So this is the diameter of the stem. And this is the neutral axis here in the middle. The strength goes as that solid line there. It goes as the fourth power. And the stress goes as that dashed line there, as the sixth power. So they're not exactly on top of each other, but they're very close to being on top of each other.

So basically what the palm has done is it's arranged the material in such a way that the strength matches the stresses that are applied to it. So if I just had a constant density, my stress profile would look like that. And if I had a constant density, the strength profile would kind of like that. So the strength here would be a constant, and this would be the stress here.

So the stuff in the middle, it's much stronger than it needs to be. Whereas the palm has arranged things so that it's got just the right amount of strength for the stress, as a function of the radial position. So it's kind of a clever thing. So that's kind of a beautiful thing. And I think that is it. I think that's-- yeah, that's the end of it.

So all these images came from this other book that we wrote. And if you wanted to get the sources, you could get them from there. So that all I wanted to talk about today was some examples of sort of efficient mechanical design in nature and the sandwich panel structures as one, and these radial density gradients is another.

We have a project on bamboo right now, and the bamboo also has a radial density gradient, and it's the same thing. The densest material's on the outside, and the least dense is on the inside. So I think I'm going to stop there for today.

So what I was going to do on Monday is talk a little bit about bio-mimicking. And that won't take the whole class at all. And I thought we could spend the rest of the class on Monday just doing a review. So the test's on Wednesday. So if you want to bring questions, that would be a beautiful thing.

I can't really can I review the whole last six weeks or something in an hour and a half or something. So if you want to bring questions, I'll be here and we can just go over questions. Does that sound good?

Free Downloads

Video

• iTunes U (MP4 - 78MB)
• Internet Archive (MP4 - 78MB)

Subtitle

• English - US (SRT)