Lec 14: Sound: External, middle and inner ears

• Download this transcript - PDF (English - US)

The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation or to view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

PROFESSOR: And I thought that what we'd do today is first go over this syllabus for audition, which is the second part of the course. Just so you get an idea of what's in store for you. And then today's lecture will have a big part on sounds, which have physical properties that are very different than the light stimulus you guys have been talking about so far in the course. And we're going to illustrate the different types of sounds, very simple sounds like pure tones. And very complex sounds like human speech, which have many, many components in them.

And then we'll get into the auditory system, first starting with the auditory periphery. And we'll talk about the three basic divisions of the auditory periphery, which are the outer, middle, and inner ear. And today we're really only going to have a chance to focus on the functions of the outer and the middle ears. And so we'll talk about the functions of those structures.

So as far as the syllabus goes, each of the lectures has a title. So today's title, October 28th, is sound, external, middle, and inner ears. And each of the lectures has a reading or more accompanying it. And so most of the readings are from the textbook. So there's a textbook, Schnupp, Nelken, and King, which is a very good, up-to-date textbook written by two psychophysicists. And one physiologist, Israel Nelken. And it's written at just the right level for this class. That is an advanced undergraduate textbook. So it's pretty easy to read, or should be very easy to read. And it's written very well. These guys are good writers. They have many examples of auditory demonstrations that you can listen to just by clicking in the margin of the text. The demonstration we'll come up.

And as you can see, after today's lectures, I like to give demonstrations. Because I like to listen to what we're talking about in terms of how does it really sound to you as a listener. So I'd encourage you to get that textbook.

Now you could buy a hard copy, or if I'm not mistaken, Michelle you can get a free copy online. Is that right?

AUDIENCE: There's an online version as well that you can read on [INAUDIBLE].

PROFESSOR: OK. Great. So if you have any trouble figuring that out, let me know. But I think you should easily be able to find the online version. And it should have the demonstrations that you can listen to with earbuds or headphones.

There is for today these passages from the textbook. And then for today and for many of the lectures, there is another reading, which is a research paper. This one is by Hofman, Van Riswick, and Opstal. And it's titled, Relearning Sound Localization with New Ears. And this we'll talk about in class right at the end of today's lecture when we talk about the function of the outer ear, the pinna, so-called.

And they did a very interesting experiment that addresses what is the function of your external ear. So people always ask me, what am I responsible for in these readings. Well this is a very specific paper. It has a lot of interesting research methods. The subjects were human volunteers. And there are a lot of details in there that are not that important.

What I'm really focused on having you learn is the take-home message. And the take-home message from this paper is, what is the function of the outer ear. And what is this twist in the title, how can you relearn sound localization with different outer ear.

We'll talk about it in class. But I want you to get the take-home message from these research studies. Because there sort of what we do as professionals in the auditory system. Our day-to-day living is doing research. In some cases on human subjects, in some cases on individual molecules. But how can we learn about hearing from doing these research studies?

And I have picked good papers, good research studies. Because they really tell us something. There's plenty of stuff out there that gives sort of equivocal results. But this is a really good paper. And you have a take-home point from it about how you use your outer ears to localize sounds. So that's an example of a research paper that goes along with this lecture.

So just coursing through the syllabus-- on Wednesday, we'll have a lecture on hair cells. Next week we'll talk about the auditory nerve, which is the nerve that sends hearing information from your ear into your brain. And we'll talk about frequency resolution-- how we can tell one frequency from another. At the end of next week, we'll be talking about the brain, the cochlear nucleus, and all the interesting unit and cell types in the cochlear nucleus. The following week, we're going to be talking about hearing loss, how there can be problems with your hearing.

Many of them are treated at the hospital where I do my research, which is Massachusetts Eye and Ear Infirmary across the river. And there, when the surgeons in my department encounter a deaf person, they give them the option to get a cochlear implant. So a cochlear implant is a device that can be put in your inner ear. And it can restore your sense of hearing. And we'll have a demonstration by that cochlear implant user who comes to class on that date and gives a demonstration of her cochlear implant, which has restored hearing to her, although not perfectly.

So then later on in the semester, we'll talk about various other topics on up through the auditory cortex. And finally, we're going to have a tour of the Hearing Research Laboratory at the Massachusetts Eye and Ear Infirmary, where we'll meet over there and we'll encounter various research projects that are currently going on. And we'll talk about them.

There is a written assignment. I guess you guys had an assignment for vision in the class-- a written paper? So we have an analog here on the auditory system. And this is the assignment you can read it later at your leisure. It won't make much sense right now, because we haven't talked about neural circuits for localization of sounds yet. You can look on the syllabus. It's about halfway through the second part of the class. And there's a lot of details here. And it asks you what's updated since an original model was postulated by a researcher called [? Jeffrus ?].

So that's a paper-- I don't think I said how long it should be. How long was the paper for vision? Was there a link?

AUDIENCE: [INAUDIBLE]

PROFESSOR: Four to six pages? OK, four pages sounds good. If you really want to write six, you probably could. But we'll talk about this when we talk about sound localization in the class. And I think the due date here is written. It's the date of the lab tour.

And then, we have a final exam in the class. And I think as Doctor Schiller talked about at the very first day, the final exam will be waited toward the auditory system, which we haven't had a test on by the time this exam rolls around. So I think it's going to be 2/3 audition on the final exam, and 1/3 vision. And there are several review sessions for both senses planned at the end of the semester.

So any questions about the organization of what we're going to do?

OK, so I'll start today's lecture. And I think the PowerPoint files-- for today's lecture and all the rest of the lectures for the rest of the semester are available in the course website. So you can look at them now or as the lecture comes up.

So first, we're going to talk about the physical characteristics of sound-- just very, very different than the characteristics of the light stimulus. And maybe light stimuli are so obvious that Peter Schiller probably didn't spend much time in his lecture about it. But I'm going to spend 10 or 15 minutes here on the physical characteristics of sound. Because it's very different than the light stimulus. So sound is a mechanical, radiated energy, transmitted by longitudinal vibrations of a m so you have to have a medium to transmit sound. You can have light go through outer space in a complete vacuum.

But in outer space, you can't have sound because you have to have a medium. The medium can be various types of things. We're going to talk mostly about sound in air. But you could have sound in water-- whales make songs, and they sing to each other, and one whale listens to another. And in between the two is a medium of water. You can have sound in a solid-- if you live in an apartment room, and you hear your neighbors' music, you especially here the base. Because the low frequency sound transmits pretty well through solids, like the solid of the wall in between the two apartments. Sound can go in many, many different types of media.

In air, like we're going to use mostly for this course, you can think of sound is being produced by a sound source like the piston of your loudspeaker. And the piston goes back and forth. . It's driven back and forth by an electric voltage and when it goes this way, it presses on the air molecules in front of it. And it presses them so they're closer together and makes them a little bit higher in pressure. And that's what's meant by this compression or condensation. And these dots close together means a little bit of an area of high pressure. Then as the piston moves the other direction, it rarefies the air. It drags some of the air with it. And so that little space right in front of the piston has a lower pressure. Because there are fewer molecules per volume than before. So this energy, then, is transmitted through the medium to whatever-- a microphone, which detects sound, or a listener, which can listen to the sound.

If you have a microphone or some kind of detector that can plot that pressure at any one point-- let's say the microphone is right at the edge of this paper. And you graph the pressure as a function of time on this graph. So here's pressure and here's time. As those radiated energy wave fronts pass you, the pressure will go up. And then it will go down. And then it will go up and go down. And it will repeat over and over as long as that piston moves.

So this horizontal line is simply the barometric or static pressure of the air. And sure, the barometric pressure changes a little bit. If there's a hurricane coming, it gets way low. If there's a high pressure like we have right now-- sunny climate, the barometric pressure goes up. But those are very slow fluctuations. And the sound wave form is a very, very fast waveform that goes many times per second.

In fact, what we call as sound frequency is the number of oscillations of that pressure wave per second. And they are very fast. As you can see down here on this so-called audiogram or frequency curve for human hearing, the frequencies, which are on the x-axis here, go from 10 Hertz-- Hertz means cycles per second-- so one Hertz is one cycle per second. And that is a frequency that's so low it didn't get on this graph. Because humans aren't sensitive to frequencies that slow or that low. Usually the lower limit for human hearing is considered to be about 10 cycles per second, or 10 Hertz. And it extends all the way up to 20,000 cycles per second. And in the middle of the human range, we'll be talking about hearing a lot at a middle frequency of about 1,000 Hertz. So that's a nice, round, middle frequency for you to remember for human hearing.

So we're talking about pressure oscillations in terms of thousands of times per second, or hundreds of times per second. So they're very fast. There will be examples during our course where the auditory system-- the auditory neurons keep track of those cycles, even though they're going back and forth thousands of times per second. So we'll come back to that in future lectures. Now this is the audiogram for human hearing in the solid curve here. This is supposed to say human, if you could read it. And on the y-axis is how strong the stimulus is, how loud it is, or in terms of physical characteristics, what the sound pressure is. And this scale goes from minus 20 to 140.

And the units are dB SPL and that stands for decibels sound pressure level. And whenever you hear level in a formula, you should perk up your ears and say oh, that means there's a log-- a logarithm-- in the formula. And sure enough, the formula for a sound pressure level is 20 times the log of whatever sound pressure you're talking about, whatever you were listening to or measured by your microphone divided by some reference pressure. That's the formula. And the reference pressure is given as 20 micronewtons per square meter. OK, so let's figure that out. What is Newton a unit of? Anybody?

AUDIENCE: Force.

PROFESSOR: Right, force-- and meter squared is area. So we're talking about force per area, and that's pressure. So Newton obviously was like Hertz, one of the people who was interested in physics. And a Newton is a unit of force per square meter is pressure. Now in more modern terms, the unit micronewton per square meter has been renamed to be a pascal, abbreviated Pa. So it's the same. One Pascal is one Newton per square meter. In this case, we're talking about micro-- Newtons are micro Pascals. So why is that number chosen as the reference for this very important sound pressure level scale? Well, it's actually chosen with the hearing system in mind.

What they did in the 1930s, when this was being developed, is they rounded up a bunch of people at a county fair, gave them headphones, and said we're going to try a nice mid-frequency. Let's try 1,000 Hertz. They gave them a tone at 1,000 Hertz. The listeners listened to it. Then they said I can hear that fine. Then they turned the level down a little bit. And the person said yeah, I can still hear that. Then they turned it down so much that the person didn't say, I hear something. There were silent. They turned it up a little-- says yeah, I hear-- They turned it down. They titrated the levels until it was right at threshold, just barely detectable. And they took an average of 30-some people. And they said that is going to be the basis of our sound pressure level scale. So it's actually a term that was derived biologically by testing people's hearing.

So that's kind of a nice story. I wonder if it's true. Well, let's look at it. Where does the human hearing curve, that 1,000 Hertz, fall? Where should it fall if 20 micronewtons per square meter is the pressure you're talking about? It's the same as the reference pressure. What's 20 over 20? It's 1. What's the log of 1? Zero. Correct. 20 times the log of 1 is 0-- sound pressure level 0. Well, look at our curve right here, that 1,000 Hertz-- it's pretty close to 0. Why might it not be exactly zero? Well the people that were used for this curve were a little bit different than the ones in the county fair. We'll study later on that some people have a hearing loss.

Hearing can be affected by the room that you used. Maybe there was a lot of yelling and screaming at the county fair. We have better rooms to test hearing now. It turns out that the human hearing curve is actually a little more sensitive at 2,000, 3,000, and maybe 4,000. So when the pressures go below the reference pressure, the number becomes less than 1. And the logarithm becomes negative. It's perfectly fine to have a negative SPL. We have some points on the graph for that-- minus 2, minus 3 dB.

This other dashed audiogram, or hearing sensitivity curve, is for a different species-- the cat. And the cat here's down to about minus 10 dB SPL-- at least this group of cats did. The cats also hear higher in frequency than humans. Dogs and cats can hear about an octave higher-- that is a doubling of frequency higher than humans do, and maybe some of you have had dog whistles that you blow. And you don't hear anything. But the dog comes because it's a very high frequency beyond the upper limit of human hearing, but well within the hearing range of those species. So different species have different hearing ranges.

AUDIENCE: Professor?

PROFESSOR: Yes.

AUDIENCE: Sorry-- just to clarify, is a micropascal then [INAUDIBLE]?

PROFESSOR: No. These are units of pressure-- micronewtons per square meter-- and this is a unit of pressure. SPL is just in these units called decibels. And it it's not a pressure--

AUDIENCE: It's the log of that.

PROFESSOR: That's right. It's the log of that. Any other questions?

So these are sort of the lower limits of hearing. When you go into conversational levels, or the level of a lawn mower, or the level of a concert, the levels get higher-- still certainly within your audibility range. As you go to a higher and higher level, you risk damage to your hearing. And at that risk level, which it says high risk thresholds here. And right around 120 dB, sounds become painfully loud and damaging to your hearing. And that's what this shaded area refers to-- gunshots, jet aircraft engine. And we'll talk about that during our lecture of hearing loss.

So I have some demonstrations. Because a lot of people have trouble with the decibel scale. So what is a decibel? And what does it sound like when you change the sound from 50 dB to 60 dB?

Well this demonstration has three parts. And let me read the text first. Broadband noise-- sometimes it's called white noise. Broadband noise and white noise are synonyms. And what is white light as a visual stimulus?

AUDIENCE: All wavelengths.

PROFESSOR: All wavelengths, right? And so broadband noise means it has all frequencies. It has 10 Hertz, 20 Hertz, 30 Hertz, 1,000 Hertz, 2,000-- it has all frequencies. And it sounds like the "shh" sound. So you hear this "shh." it'll start out pretty loud. It'll be reduced in ten steps of six decibels for each step. And I think you'll be able to very clearly hear the difference between the first and the second steps. And demonstrations are repeated once.

The second demonstration is same noise is reduced in 15 steps-- now of three decibels. So this is a little bit of a smaller scale, though you'll still be clearly audible. Third, broadband noise is reduced in 20 steps of now one dB. So let's listen to see if we can hear 1 dB steps.

RECORDING: The decibel scale-- broadband noise is reduced in 10 sets of 6 decibels. [INAUDIBLE] repeated once. [TONE] [TONE]

OK, was that clear-- the difference between one and the other? So that's what 6 dB sounds like? Now, you guys who are up here close to the speakers, you might be starting at 85 dB SPL on the first ones-- pretty loud. 6 dB lower is 79. And then, so on and so forth. You guys at the back are further from the speaker. You're not starting at the same level. You might be starting at 60 dB. You're still going down 6 dB to 54 dB in the next step. Everything is linear in here. It doesn't matter where you start from, as long as you're going down 6 dB. So where you start doesn't really matter in these demos.

RECORDING: Broadbad noise is reduced in 15 steps of 3 decibels. [TONE] [TONE]

PROFESSOR: OK, still clear the increment between one and the other? OK, now here's the one dB steps.

RECORDING: Broadband noise is reduced in 20 steps of one decibel. [TONE] [TONE]

PROFESSOR: OK so how about for that? Would you be able to stake your life on the fact that you could tell one from another? No, I see a lot of heads shaking. Well if you sit there and do this over and over again, and really train yourself, apparently 1 dB is the just noticeable difference that most observers can here. So 1 dB is the just noticeable difference in SPL.

So how do we do that? Well you have an auditory nerve. And at 60 dB, your auditory nerve fibers are sending this many spikes to the brain. At 61 dB, they're sending maybe a few more spikes-- something like that. It's not absolutely clear how you do that. There is more information coming in from the ear to the brain as a function on sound level. We'll talk a lot about that.

Now, we also talked about sound frequency. JND for sound level is about 1 dB. What is it for sound frequency? We're going to have pretty much a whole lecture on that. But your ear is extremely good at telling one frequency from another. So if you start at 1,000 Hertz and change it to 1,002 Hertz-- very, very small change-- you can tell the difference. Your ear is a fantastic frequency analyzer. We're going to have a whole lecture on exactly how your ear does that. But the JND for sound frequency is also a good demonstration. We'll play that when we talk about sound frequency coding.

OK. Any questions about that so far?

OK. Let's switch back to the physical characteristics of sound. And these are some very common auditory stimuli. We've heard a noise just now. And if you graph the sound pressure as a function of time, this is what the waveform looks like. How could you do that? If you take a microphone, stick it out in front of a noise source, and run that into an oscilloscope, the microphone converts the sound pressure into a voltage, the oscilloscope displays the voltage signal as a function of time. You can look at that.

Auditory scientists like to look at things as a function of time, of course. They also like to look at things as a function of sound frequency. This is a graph for this same stimulus, a noise stimulus, now as a function of frequency. And we said before, the noise is broadband. It's white noise. It has all frequencies. And here is the graph to show you that. This might be the energy, and this is as a function of frequency. So it has all frequencies. It's trailing off a little at the very highest. That may be because the microphone couldn't wiggle back and forth at very, very high frequencies. But it's essentially a flat frequency curve.

And sometimes this display is called the spectrum. So spectrum or spectra are graphs as a function of frequency. Sometimes people talk about this as a frequency domain and the time domain. If you've taken any electrical engineering courses here at MIT, people will talk about the time and frequency domains. And how can you go from one representation to another? Well, you can take your microphone signal instead of going to the oscilloscope, going to the spectrum analyzer, which is a machine that can give you this nice plot.

But how about mathematically? How can you do that? The Fourier Transform, right. Of course, Fourier was a mathematician who studied various things, heat transfer and other things. He developed this transformation. If you have the mathematical description of a time-varying signal, you can plug it through his equation, the Fourier transform, and come out with the frequency representation or the frequency domain. Or, vice versa, if you have the frequency domain, you can inverse Fourier transform and go back to the time domain.

We're not going to talk too much about transforms here. But it is interesting, because, as it turns out, your inner ear is a wonderful frequency analyzer. It can tell the difference between 1,000 and 1,002 Hertz. This is a very nice way in the ear of detecting the different frequencies. And so these time and frequency domain representations are very convenient for us to look at. So just keep that in mind.

Here's a very common auditory stimulus, the pure tone or the sinusoid. This is a sinusoidal waveform in the time domain. In the frequency domain, it only has one frequency-- the frequency at which that thing is going back and forth in terms of Hertz. This is in a Hertz axis. So sometimes it's called a pure tone. Why is it so pure? Does it have high morals or what? No, it just has one sound frequency.

These other stimuli, we're going to listen to this in just a minute. This is a so-called square wave. Imagine trying to add up a whole bunch of pure tones to result in a square wave. It seems impossible, right? Well, it's possible if you use an infinite number of frequencies. And this frequency representation for a square wave goes on basically forever. To get those corners of the square wave sharp like a true square wave, you need lots of individual frequencies, lots of pure tones, if you will.

Tone bursts are some common auditory stimuli. We'll talk about those later in the course. Click is a very common auditory stimulus. It's a sound like this. Or last night, it was the sound of a fastball hitting a wooden baseball bat. It's a very sharp, impulsive sound, very nice sound if you're behind the team who's batting. So a click, that baseball hitting the bat, doesn't happen for very long. A click can be infinitesimally short. The time that the baseball is in contact with the bat is pretty short. And if it's very short in the time domain, then you have all frequencies. So it's another example of a broadband or broad spectrum sound. If the click is infinitesimally short, the spectrum is completely flat.

Those are some common auditory stimuli. Let's go through some more complicated, and maybe more interesting, sounds. Well, all of us like to listen to music, right? So here are some examples of musical sounds. This is a piano keyboard. And here is the spectrum or frequency representation of what you get when you strike one key on the piano keyboard. So that's one note. Well, sure, it sounds like one thing, but you have a whole bunch of different frequencies that go along with it. And why is that true? Does anybody know? Why do you get a whole bunch of different frequencies when you strike a key on the piano keyboard? Yeah?

AUDIENCE: Isn't it vibrating all along the length so there's different wavelengths?

PROFESSOR: What's vibrating--

AUDIENCE: It's not--

PROFESSOR: In the piano?

AUDIENCE: It's not-- it's like an infinitely small portion of the string. It's the longer string. It's parts that are shorter still vibrating.

PROFESSOR: Yeah, you're getting there. In the piano, the string is fixed at one end, and it's a long string. It [? fits ?] [? in ?] the other. And your key that you press down makes a hammer go up, and there's a bunch of linkages. And eventually, the hammer hits that string somewhere. And the string, it's fixed here. It's not going to move. It's fixed here. It's not going to move. But in between those points, it can move. So it can vibrate like this, or it can go up and down. It can also vibrate like this.

You can have what's called a node in the middle. In fact, if you put your finger right here and fix that middle, it wouldn't allow the string to vibrate in this uniform fashion. But it would allow this half to vibrate and that half to vibrate. This node is sort of a constraint for this string. It can also vibrate like this.

I wish I had a different color. Over here? Great.

OK. You can also have the string vibrate like this. OK. And it can vibrate in many, many different patterns. I've just drawn a few. What's interesting is that this length is twice as long as this length, which is twice as long as this length. And what would you expect the time of those vibrations to be? Well, the big long thing is going to vibrate pretty slowly. That's what's called the fundamental frequency.

The thing that's vibrating in two parts, it's shorter and it can vibrate faster. In fact, it vibrates twice as fast. So the first harmonic is twice the frequency of the fundamental, and so on and so forth. You can get from the physical characteristics of the vibration of that string a whole bunch of different vibration patterns. And they're usually a harmonic series-- twice, three times, four times, five times, six times-- the fundamental, just because of the physical characteristics of vibration of the string, and the wind column in the case of an Alto saxophone.

When you hear that one note hit by the hammer, all of these vibrations are happening at once. And so that one sound sounds like one thing. Musicians will say it sounds like a note-- A above C. But you have a whole bunch of different harmonics in it.

What is pitch? Pitch is very interesting to people who study the auditory system, to musicians. Pitch is that attribute of the sensation, auditory sensation, in terms of which sounds can be ordered on a musical scale. Let's say I didn't let you see the keyboard, but I recorded the sounds, and I press some sounds down there, some in the middle, some way up here, some way at the high end, and I gave you 20 different recordings, and I said, well, make a ranking of them. Put these down low. Those are number one and two. Put these in the middle-- those are number 10-- up to the high end. The highest one is 20. You could do that. The ones that were down low would be called those with low pitch.

The pitch of a pure tone, of course, depends on the frequency. That's as if you were just giving one. If you move that around, up high end frequency, it sounds like a really shrilly, high-pitched sound. If you move it down low, it sounds like a real low sound. The pitch of a complicated sound-- that is, with many overtones and harmonics-- depends strongly on the fundamental frequency. But sometimes, the fundamental-- for example, in this guitar sound-- is pretty weak. And in some cases, you can take it out altogether. The pitch doesn't change that much, surprisingly. So somehow, the ear knows by this pattern of spectrum that there should be a fundamental [INAUDIBLE] that can stick it back in.

So that's what pitch is. Another sensation that musicians often talk about is the timbre of a sound. And the timbre is the quality or the identification of a sound. It relates to the highest harmonics here and the pattern of this harmonics. For the piano, it's starting big and sloping down. For a guitar, it's starting small, sloping up, and then sloping down. The timbre is what allows you to identify that sound that you heard as a piano. We can all hear a piano and say, that's a piano. We can all hear a guitar and say, that's a guitar, or that's an electric guitar, because its pattern of harmonics, its fundamental harmonics, differs. That's how we identify sounds is by their timbre or their spectrum, if you will.

Those are pretty complicated sounds. What do I have next? I have a demonstration. This one is called Canceled Harmonics. And it's a very nice demonstration to illustrate the idea that I said, when you have all these harmonics go on together, it sounds like one thing, one note, one sound. But if you take some of the harmonics out and put them back in, you're aware of that taking out and putting back in.

So what they're going to do is a complex tone is presented, followed by several cancellations and restorations of a particular harmonic. And let me show you what complex tones they're going to give you. It's simply this square wave. This is what you're going to be listening to. It sounds like [MAKES BUZZING NOISE]. It's not very musical at all. And it has a fundamental and a whole bunch of harmonics, an infinite number.

When that complex goes on at once, you're going to say, that sounds like a nasty sound. It sounds like a buzz almost. Then they're going to take this one harmonic and pull it out, and then they're going to put it back in. As they do that, you're going to say, well, that sounded differently. When it was out and when it was back in, I could hear that thing going in and out. And then they're going to do that for the second, third, and fourth on up to, I think about 10 or so.

Even though this whole constellation sounds like one sound, when they pulse these things in and out, you can tell. Let's listen to the demonstration, and let's see how many times they're going to do it. This is done for harmonics one through ten.

Canceled Harmonics. A complex tone is presented, followed by several cancellations and restorations of a particular harmonic. This is done for harmonics one through 10.

OK. Could everybody hear when this complex went on all at once it sounded like one sound? Then when individual components were taken out and pulsed back in, you could identify them. Your ear is very good at distinguishing the various frequencies in a complex spectrum. All that message is sent to the brain as individual channels, and the brain somehow perceives that when everything is going on at the same time, that's one sound. It's really not of interest to the brain that the string is vibrating a whole bunch of different frequencies. It's that there's one string vibrating.

But if you took out one of these modes-- in other words, if I put my finger here and the fundamental goes away, you ear is very good at detecting that. And it sends a message to the brain that the fundamental is no longer there. And the brain says, something different has happened. So the ear is very good at recognizing those different characteristics. The brain is good at putting them back together and saying, they started at one time, so it's one object.

Questions about that so far?

Now, the last type of complex sound that I want to cover is speech sounds. And I want to save most of this for the end of the semester when we talk about the parts of the auditory system that are active in distinguishing different speech sounds. But let me just-- because we're talking about sounds and complex sounds, talk about speech sounds.

This is a diagram of your vocal cavity. Way down at the bottom here, you get air from your lungs that goes through your trachea. And in the trachea, there's these vocal cords, if you will, that are scientifically called the glottis. The opening in between is the glottis. So air can come out, or if you use muscles associated with your vocal cords, you can close that off.

As the air comes out from here, it moves those vocal cords back and forth. And they hit each other, and they open up, and they hit each other and open up. And as they do that, they interrupt the airflow and they allow it to pass through. And they interrupt it, and they allowed it to pass through. And if you were to put a microphone way down your trachea right above those vocal cords, you would see this time waveform. The pressure would go up right as the air pressure is coming from the lungs when the vocal cords were open. When the vocal cords are shut, there's no pressure there, or it's just atmospheric pressure.

So this opening and closing of the air through the glottis forms this very complicated waveform. If you look at the spectrum of it, it has a whole bunch of different frequencies. The lowest of the frequencies is the frequency that these things are opening and closing. But there's a whole bunch of harmonics. It's a very complicated spectrum.

The upper part of your vocal tract is what's called the filter. And it serves to emphasize some of those harmonics and de-emphasize others. And the filter function is indicated here having three peaks. Those peaks are called formant peaks. They have to do with the shape and dimensions, lengths and widths of your upper vocal tract. What's kind of neat is by manipulating, let's say, where your palate is, and where your lips are, and where your tongue is, you can change that filter function by using the muscles that move things around in your upper vocal tract.

And after you've filtered this complex spectrum, you come out with a function where some of these spectral peaks are emphasized and some are not emphasized. And here's the function that you would get right outside in the air outside the front of your mouth. This is the time wave form here.

Here are some examples of manipulation of your upper vocal tract. For instance, here the lower part of the mouth is moved way up high, and it produces an acoustic spectrum where you have a big f1. And f2 and f3 are small, and they are way up high in frequency. Contrast this with when the bottom of your mouth is lowered and moved backward. Here, F1 is even lower. F2 is quite low. And F3 is moderately low.

And these are, of course, the way you pronounce different vowels. We can all say these two vowels. This is the vowel "i" as in "hit." Everybody say that-- hit, hit. You can kind of feel that the lower part of your mouth is moved upward. Whereas if you do something like this-- "a" in call. Call-- everybody say that. Call. You can feel the lower part of your mouth dropping down as indicated here in making a big cavity, whereas here the cavity is very small. It changes the acoustic spectrum. Our ears pick it up.

And our ears are very good frequency analyzers. And they say the spectrum here sounds like hit, because you've learned to associate that spectrum with that vowel. This is a different spectrum. Our ears pick it up and they say, that's the vowel "a" as in "call."

That's how speech sounds are formed. At least this works very well for vowel sounds. It doesn't explain things like consonant sounds, which of course are many different kinds. There's stop consonants where your lips close down before you utter the consonant "p." So "p," everybody close their lips down, and then all of the sudden you open it up. It's a completely different thing. That's not modulating the spectrum. That's modulating the time pattern. These vowels are distinguished by their different spectral patterns, which is picked up by your years.

So I just thought you'd want to know about that. Speech sounds are among the most complicated acoustical sounds because of the number of frequencies involved, the formation, and of course the perception of telling, for example, one vowel from another.

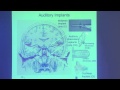
Let's shift gears and move on. And instead of talking about the physical characteristics of sound, let's talk about how we hear sounds. We're only going to get as far as the auditory periphery today, but let's just define it. The auditory periphery is this whole structure indicated here, and it's usually separated into three parts-- the external ear, the middle ear, and then the inner ear. Those are the three very big divisions of the auditory periphery.

In the external ear, you have your pinna. Here's your pinna. You have the ear canal, which goes down about three centimeters inside your head, and it ends up at this yellow structure here called the ear drum. Tympanic membrane is the scientific term for the ear drum. That's the end of the external ear. The middle ear is an air-filled cavity. So we're still talking about sound in the ear. In that middle ear cavity are three small bones. They're called ossicles.

I think-- yeah, here we go. And in high school biology, you probably learned them as hammer, anvil, and stirrup. But the scientific names are malleus, incus, and stapes. And they convey these sound vibrations of the ear drum. When sound hits the ear drum, it causes it to move. And these bones are linked right onto the eardrum, and they're linked one to another. The ear drum then moves the bones, and the bones finally end up, in the case of the stapes, in the inner ear. So that's where the inner ear begins.

I have a demonstration of ossicles, and I'll pass them around. These are ossicles from a guinea pig, and they're glued to the bottom of this little vial. And I made a crummy drawing of them. But if you hold this vial so that the piece of tape on it is downward, you get this view here. You have the stapes. And I didn't list the other ones. But in the guinea pig, the incus and malleus are fused, so they can be considered one. This is definitely part of the malleus. But I don't know where the incus ends and the malleus begins. If you had an ear drum, it would be this dashed line here.

So let me just pass these around. And you can probably appreciate from my diagram how the high school biology name for the stapes got its name. It's the stirrup.

What's the stirrup? Does anybody know what a stirrup is?

Yeah. When you ride horses, what is the--

AUDIENCE: You put your foot in it.

PROFESSOR: You put your foot in it. And that's why cowboy boots have a nice big heel, so your foot doesn't go all the way through it. It sticks in your heel. So this is the stirrup. You put your cowboy boot right in there until your heel hits this foot plate. That's pretty obvious how that got its name. It's the foot plate where you put your foot. Your foot goes right on that.

And that foot plate is the beginning of the next division, which is the inner ear. And by the way, I should point out before I forget-- what is the smallest bone in the body? All answers are given. The stapes is the smallest bone in the body. Why? It's got to move. And the lousy little sound-- it's this tiny little ear drum.

Remember, the ear drum is basically a tiny, little thin piece of skin. It's like Saran wrap. When your doctor looks down your ear canal, that doctor can look right through the ear drum. It's so thin. It's like plastic wrap. The doctor can look into the middle ear and say, so much fluid in there. You've got a middle ear infection. Or they can say, middle ear looks good. You've got some other problem. That's what we're looking at. They're looking with their otoscope and a light right through the ear drum into the middle ear.

And that whole middle ear drum and the ossicles have to vibrate when there's a tiny little sound like a pin drop. The pin drops right there, and you can hear it because these things are so light and flexible that they can vibrate-- and so small.

The stapes foot plate ends up at the cochlear. And the cochlear is the main part of the inner ear. And cochlear, as it says here, gets its name from the Greek word kochlias, which means snail. And certainly, the inner ear looks like a snail shell. And in the inner ear, here's where sound changes from sound in air, or maybe sound in the bones. The inner ear is filled with fluid.

And inside the inner ear are these wonderful receptor cells for hearing and the beginning of the auditory nerve. Here's the auditory nerve that's sending messages centrally into the brain. So the brain would be beginning right here. This whole structure here, all this gray stuff, and even the shell of the cochlear is bone. And it's your temporal bone. The temporal bone is the hardest bone in the body. You can have a severe blow to the head and that temporal bone will keep all these structures intact. It's very, very hard bone. Surgeons at our hospital do a lot of drilling with the dental drill. They get down to these important structures, because they have to manipulate them.

These loops here are part of the inner ear, but they are part that is sensitive to vestibular sensation. So those loops are called the semicircular canals. They are almost circular. They are in the three planes, X, Y, and Z. And when you rotate your head, let's say, side to side, one of those can move. And the receptor cells in it can sense that movement and detect that your head had moved. And it's very important, because if you want to keep your eyes fixated on one point but move your head, you can do that by the vestibulo-ocular reflex.

The neurons from this the vestibular system send messages into the brain stem, and eventually they go through coordinating centers into the motor neurons for the extraocular muscles, which can, of course, move your eyes when you want to do a [? secade ?] or pursuit, or they can keep your eyes stabilized, which is moving them with respect your head even though your head is moving. But we're not going to talk about those.

Let's talk about the function of the middle ear and the external ear. That's what we're going to talk about for the rest of today.

I have a model. Let me just pass around this model. I think we passed around before on the first day of class, but you can look at it again, because we're going into more detail today on this structure.

This comes apart. Here's your pinna. Here's the long ear canal. Here's the ear drum. And if I tilt this here, you can see the structures we're talking about in the inner ear-- the cochlear, the semicircular canals, and this yellow structure here is the auditory nerve. It's been going into the brain. The brain is cut off here. This is the eustachian tube, which is a way to vent the air-filled middle ear. So you want to purge that with air. If you go up hiking in a tall mountain, the barometric pressure outside gets lower. You want to equalize that in your middle ear. You open that eustachian tube, usually by swallowing.

The ossicles are here. And if you take out this inner ear, the stapes is fixed with it. So you can see the stapes. In terms of size, this whole inner ear-- the cochlear is about the size of an aspirin tablet in a human. It's about that size. OK. Let's pass that around.

OK. What is the function of the middle ear? Why do we have these three bones? Why do we have the eardrum? Why doesn't sound come right in and strike the inner ear itself?

Well, it turns out that if you look at the physical characteristics of sound in air, and you want to get that airborne sound to sound in water, different medium. So this is fluid or water. This is air. Sound is coming in here, and you want to get it into the fluid of the inner ear, which is essentially water. If you don't do anything and you have the sound coming in here, most of it bounces back off. In fact, 99.5% of the energy of sound in air at a fluid boundary is reflected back into the air.

So if you're in a boat here-- I didn't draw this right-- you're in a boat here, you're fishing, you're talking to your buddy in the back of the boat and you say, pass me another beer, and your buddy says, be quiet, you'll scare the fish-- actually, the fish can't hear you. Because most of the energy in your saying "pass me a beer" bounced right back off into the air.

So how does the auditory system deal with this? We want to listen very carefully to a pin drop, but most of the energy bounces back off at this boundary between air and fluid. That's the job of the middle ear.

Here is how the middle ear moves. This is a nice movie made by Heidi Nakajima at Mass Eye and Ear Infirmary. This orientation is a little bit different, but this is the ear drum. This is the malleus, the incus, and the stapes. Together, they're the middle ear. I said this inner ear is the cochlear here, and it's encased in bone-- fluid encased in bone.

So how does this stapes work? Well, there's a little window in the bone. It's called the oval window. And the foot plate of the stapes pushes on that oval window. It's not indicated here, but it's right underneath this oval part.

There's another window called the round window. That's indicated by blue there. And it's just a pressure relief point, because if you pushed on fluid, it would push back to you. Fluid is relatively incompressible. So this pushing in means this membrane over the round window can push out easily. So it's easy to push in and pull back, because this membrane can give.

As you can see, the motion of these bones is coming into the fluid quite nicely and changing some membranes inside the inner ear. The job of the middle ear is so that most of that sound energy gets into the fluids of the water of the inner ear. How does it do that? The primary way is by changing area. The eardrum is this big drum, and the stapes foot plate is this much lower in area or smaller structure.

And there's some formulas here. p1, a1, those pressure and area at the tympanic membrane, equals p2 a2 where the same characteristics at the stapes foot plate. So when you decrease the area a lot, a2 goes way down. p2 has to go way up. So that's then the main way that the middle ear allows sound and air to go into sound and fluid.

The engineers would call this impedance matching. And they would say that when you change media, the impedance of one medium being different from another means that most of the energy is going to bounce back off. If you have a device here like the middle ear to make the impedances more matching, much of this energy is going to then go through the boundary from one medium to the other if you match the impedances. And one way of matching the impedances is to change the areas.

Another way-- and this may be the reason we have three and not just one middle ear bone-- is by a lever action. So this is kind of like a lever where the fulcrum is off to one side, not right in the middle. And you can obviously get force amplification from a lever action. A third mechanism might be a buckling of the tympanic membrane. And you'll have to read-- I'm not an expert on that at all. I'm not even sure if that's even in vogue these days. But these actions are much less than the change in area offered by the eardrum.

So what happens when a patient comes into the Massachusetts Eye and Ear Infirmary, and for some reason, either via an accident or a developmental problem, they don't have an eardrum, and they don't have these three ossicles. So the sound goes right in from the outside and strikes, let's say, the round window of the cochlear. Are they deaf? Well, no. They have a hearing loss. Some of the energy gets through into the fluid.

How big is their hearing loss? Well, this is the so-called audiogram that's generated when you visit a hospital and you complain that your hearing isn't so good. They send you down to the Audiology Department. They put you in a testing booth. They put earphones on, and the tester goes outside so they don't make any extraneous noise. And they say, raise your hand when you can hear a sound. So they test your hearing-- this is the so-called audiogram-- and plot it on the y-axis as the amount of hearing loss in decibels. It's just the way they plot it. And plot it on the x-axis as the frequency.

And they typically test 2,550, 1,000-- which is abbreviated here 1k-- 2k, and 4k. They typically don't test the extremes of the human hearing. They test the middle range. This is the range over which most speech sounds are made. And that's the most important for most people. When they say, I can't hear very well, it means they can't understand somebody when they're speaking.

And this is the audiogram from someone who lacked a middle ear. And this 40 dB here-- across all the different frequencies, approximately 40 db-- is the amount of hearing loss they have. So if you go back to the audiogram that we had in the first slide of today's lecture, everything would be lifted up by 40 dB. You have a 40 dB hearing loss. You're not deaf at all, but that's a moderate to severe hearing loss, a 40 dB hearing loss. You might have problems-- you certainly would have problems hearing a pin drop. You might have problems hearing a telephone ring if it were on the other side of the room. You might have problems with conversation.

A treatment to that would be several types of treatment. The surgeons in the Ear, Nose, and Throat Department at Mass Eye and Ear could reconstruct your middle ear and your eardrum. They could use a skin flap, a piece of skin taken from somewhere else on your body, put it in the place of the eardrum. They could use some either wire or Teflon or plastic pieces that could connect that eardrum into the oval window of the cochlear. So they can reconstruct the middle ear fairly easily.

If the person doesn't want to have surgery, they can have a hearing aid. Essentially, you have a flat frequency loss here. So put a device in the ear canal that boosts every single frequency by 40 dB, amplify the sound. So a hearing aid works pretty well for these people with this type of a hearing loss.

This type of a hearing loss is called a conductive hearing loss, because it's in the conductive mechanism to conduct the sound from outside your body into the inside of your body. It's a conductive hearing loss.

So that is the job of the middle ear-- to ensure efficient transmission of sound in air into the fluids of your body. And without it, you have a moderate to severe hearing loss.

There's a disease called otosclerosis. "Oto" meaning hearing. My department at Harvard Med School is otology and laryngology. Otology and laryngology. And sclerosis means hardening or rocky or bony growths.

And the surgery that happens-- sometimes around the stapes, bony growths can grow around it and fix the foot plate so that it can't vibrate anymore. So what's done for that is you take out the stapes, you take off the bony growths, and if you just put the stapes back in, often these bony growths grow again. So actually you take it out and replace it with an artificial stapes. And the operation is called a stapedectomy. The "stape" and "ectomy" means taking it out. You replace it with a prosthesis. It's a very successful surgery for otosclerosis, which is a conductive hearing loss.

That's the job of the middle ear, and that's relatively easy to treat when there's a problem. Is there a function of the external ear? Well, a lot of textbooks say the external ear funnels the sound into your ear canal. But there is another function of the external ear that's more on the lines of localizing sounds using your external ear.

These are examples of external ears-- our pinna. Everybody has a slightly different one. Who is this historical figure? Anybody? He was a president of the United States. LBJ, President Johnson. He was always caricatured by the political cartoon guys with these huge ears, big pinnae. Everybody has different shaped pinnae.

It turns out that the external ear can help you localize where sound is coming from. Well, how can it do that? Well, if you have a pinna and you do this interesting experiment-- you take a microphone and put the microphone inside here. So here's the pinna. Here's the ear canal.

Put the microphone out here, and start out with a completely flat spectrum, broadband noise. The noise is absolutely flat so that it has equal energy at all the frequencies. You measure it out there, and then you move your microphone down here in the ear canal, maybe near the eardrum , and measure the spectrum again. So this is plotted in terms of gain with respect to free field. Free field is out here. Free field means basically in the room or in the environment.

Now we're going to measure the spectrum down here and plot the gain. So anything above 0 is going to be higher than in the ear, and everything below 0 is going to be lower. Let's look at this solid curve here, which is minus 15 degrees elevation. Elevation of a sound source-- if it's straight ahead, it's zero. If it's minus 15, it's 15 degrees below zero. If it's above zero, it could be 15 degrees. On this case, it's 7.5 and 30. So elevations that are positive are above you.

As that sound source moves around from being below you to above you, its spectrum changes, the spectrum way down here at the ear drum. And in particular, there are some very sharp dips or nulls in the spectrum that move around. It's thought that you can use those nulls as a cue to where this sound is.

Now, what causes those nulls? Well, because the pinna is very complicated, you can imagine that some sound comes in and strikes the pinna and reflects off it. And maybe it reflects-- excuse my artistic abilities here-- maybe it reflects into the ear canal. Contrast that with other sound that comes straight in. Eventually, these two sounds are going to meet up at a point. And let's say this sound taking a longer time path went through half of its cycle. So now this sound, when it's starting to go a negative pressure, meets up with this sound, which came straight in and is starting to go in a positive pressure. Positive plus negative could sum to zero.

And the geometry has to be just right, and the frequency has to be just right. But it can be just right at a particular frequency, and that's what causes the nulls. It's just a physical characteristic of two sound sources meeting up.

It is thought, then, that you can learn the position of those nulls, especially, to be associated with positions of sound in space. And that's what was done in the researchers' report for today. These are some data from four different subjects. They tested the subject to localize sounds coming from in front of them. Left and right would be azimuth. That's plotted on the x-axis. Up and down would be elevation. That's plotted on the y-axis. And they move to sounds around to different places, and they said to the person, tell me where the sound is coming from.

The answers that the subjects gave are in these solid, thick lines. The real positions were on the thinner lines. And each big individual data points are the small points, and the average data points from the subject are the big points here. So these subjects, when given a checkerboard of locations, they could pretty faithfully tell the investigators where a sound was coming from, both in elevation and in azimuth. These are data from four different subjects.

What was done in the experiment is distort the pinna. How are we going to do it? Well, we could move our ear a little bit. What they did was they put in a little clay mold in parts of the pinna to change the shape, and they did that on both sides. As soon as they did that, these are now the answers from the subjects. Terrible in terms of elevation sensitivity, determining where a sound is coming from in terms of different elevations. Still pretty good in azimuth. There are other queues for sound azimuth that involve using two ears, which we're going to talk about extensively later this semester. The elevational localization was completely disrupted when the pinna shape was disrupted.

Have these subjects go out for a few weeks, come back, get tested again. They re-learned with the pinna molds in how to localize sounds. This is an example of re-learning or plasticity. Now the pinna cues had different nulls because the pinnas were shaped differently. They could re-learn these new cues and associate them with the same old changes in elevation that we had before. So that's why it's called re-learning sound localization with new ears or new or distorted ears. So this is an example then, of subjects learning to associate these new cues with the old sound localization positions. So that's the take home message from this research report OK questions I can also do I get on Wednesday, we'll talk about the inner ear.