
Session Overview
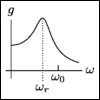 | This session looks at how the response of a system with sinusoidal input changes as the frequency of the input changes. In particular, we will want to understand the gain and the phase as functions of frequency. For the gain, which we call frequency response, we will want to find the frequency that maximizes the response. When this frequency exists we will call it the resonant frequency of the system. For undamped systems it is called pure resonance and corresponds to an infinite amplitude. For damped systems it is called practical resonance and corresponds to a finite amplitude. |
Session Activities
Read the course notes:
- Frequency Response and Practical Resonance: Introduction (PDF)
- Sinusoidally Driven Systems: Second Order LTI DE's (PDF)
- Frequency Response and Practical Resonance (PDF)
- Mechanical Vibration System: Driving Through the Spring (PDF)
- Mechanical Vibration System: Driving Through the Dashpot (PDF)
Learn from the Mathlet materials:
- Watch the video Exploration of the Amplitude and Phase: Second Order II Applet (00:11:49)
Exploration of the Amplitude and Phase: Second Order II Applet
- Transcript (PDF)
- Work with the Amplitude and Phase Second Order II Applet
- Read about how to work with the Amplitude and Phase: Second Order I Applet (PDF)
- Work with the Amplitude and Phase Second Order I Applet
- Read about how to work with the Amplitude and Phase: Second Order III Applet (PDF)
- Work with the Amplitude and Phase Second Order III Applet
- Read about how to work with the Amplitude and Phase: Second Order IV Applet (PDF)
- Work with the Amplitude and Phase Second Order IV Applet
Watch the problem solving video:
- Frequency Response (00:15:23)
- Transcript (PDF)
Complete the practice problems:
Check Yourself
Complete the problem sets:
- Problem Set Part I Problems (PDF)
- Problem Set Part I Solutions (PDF)
- Problem Set Part II Problems (PDF)
- Problem Set Part II Solutions (PDF)
