Flash and JavaScript are required for this feature.
Download the video from iTunes U or the Internet Archive.
Topics covered (lecture 24 - video not available): Power conversion circuits and diodes
Topics covered (lecture 25): Violating the abstraction barrier
Instructor: Prof. Anant Agarwal

Lecture 25: Violating the A...
Related Resources
Lecture 24
Lecture notes (PDF)
Demonstration: Boost converter (PDF)
Demonstration: Diode circuits and characteristic (PDF)
Lecture 25
Lecture notes (PDF)
Demonstration: Crosstalk (PDF)
Demonstration: Impedance matching (PDF)
All right. Good morning.
Good morning. So, we have some fun stuff for today's lecture, and as far as the final is concerned and so on, I'd like you to forget about anything we do today, absolutely.
So, get your mind to become a blank, and forget anything you hear in today's lecture. So, what I'm going to show you today will hopefully completely blow your minds.
And I'm not talking about controlled substances or anything. So what I'm going to do is show you a few things that behave completely and spectacularly differently than how you expect them to.
And, today's lecture is appropriately called -- OK. So, we're going to violate the abstraction barrier here, and do some fun things.
And, the important thing to realize is that in all of 6.002, we have, after all, based on some assumptions we made at the beginning of the course like lumped matter discipline and so on, we have landed ourselves in this playground called the playground of 6.002.
And, within that playground, certain ground rules apply.
OK, and our entire course depended on those assumptions being true. So, for example, the first assumption we made that brought us from Maxwell's equations to the lumped matter discipline was, or rather the circuit abstraction, was a lumped matter discipline. And there were three tenets of the lumped matter discipline. One is that the rate of change of flux was going to be zero within our circuits, not inside elements, but in the circuit itself, and second, the dq by dt was going to be zero outside the elements, and third, something we did not dwell upon in the course, but it's certainly present in the course notes is that the speeds of signals that we are going to consider are going to be much slower than the speed of light. OK, so we're going to be working in a realm where we are going to be well slower than the speed of light. OK, so starting with that, let me walk you through some examples and some fun stuff.
So, the first case is called the Double Take.
So, let me sketch out a small little circuit for you, and take a look at the expected behavior, and then show you what really happens in real life. So, the first case, I have a voltage source, and what I'm going to do is make a transition from a zero to a one.
Think of it as a step input, and through a Thevenin like resistance, I want to feed it to a circuit.
The circuit will go to an inverter.
This node goes to an inverter, and goes through some other circuits within our own design here.
So, again, remember, a step input here, and this input goes through a Thevenin like resistance, or is applied to some other circuit elements.
So, if I apply a step here, what do you expect?
You expect that, so let me call that VI, and let me call that Vo. So, if I plot VI as a function of time, and let's say this step input happens at t=0.
So let's say this is t=0 here, and let's say this is a 5V step. So, I expect that this input here is going to go to, VI here, is going to go to 5V at t=0. What do I expect at Vo?
At Vo, based on our circuit abstraction, I get a step input here. I should get a step of some magnitude here, depending on what's connected in this direction. And let's simply say that what's connected here is an inverter, and maybe other inverters at the other side. So essentially, as far as this node is concerned, it's got some wires connected to it. And at the end of the wires, it has an open circuit, an open circuit, for example, like the gate input of this inverter. So what do you expect at V nought? A step input here, and at V nought I see an open circuit.
OK, so I expect the same step at V nought: 5V.
So, that's what we've prepared you for, OK?
But, the fun thing that we're going to see, so this is what you expect, and I'll show you a little demo that is going to show you something very different.
What you're going to see is not this.
OK, you're not going to be seeing that.
Rather, I'm going to show you something that looks like this.
So, at t=0, I do see Vo looking like a step, and approximately halfway through, decides, ah, well never mind, and flattens out, OK, then says, oh, OK, and zoom, it goes back up to 5V. So, it sort of does a bit of a double take up there saying, hey, what's going on here?
And zoom, jumps up to 5V, and then it's five as you expect. OK, so this is some finite amount of time that looks like that.
OK, so try to understand what's going on.
So let me show you a quick little demo.
So that's the input VI. OK, so that's the input VI that you expect, and I won't do anything to my circuit at this point. And, go ahead.
So, let's see what happens now. There you go.
So now, I'm showing you the output here at Vo.
So at VI, there's a nice little step, and at Vo, notice that I get something that behaves like this.
OK, and I promise you, nothing we've taught you in 6.002 prepares you for this. OK, and as I mentioned at the beginning of this lecture, it would behoove you to forget about everything you learn in today's lecture for the next two weeks at least. So what's going on here?
Any ideas? Anybody?
Any thoughts? So what's up with my circuit here? It says, oh, OK, a step. It starts off and says, oh, never mind, and then meanders along at 2.5V and then says oh, step, yes, I remember, and then boom, it jumps up to 5V.
So, any theories? Any guesses?
Any wild guesses? OK, so let me draw you a little bit more of a detailed circuit, and see if you can explain what's going on here. So, the circuit that I've drawn there is not quite the circuit I have at least in terms of my wires. So, what I have is something that looks like this, VI, and this is going to step to 5V. I do have a resistance, R. This is Vo, this does go to an inverter. But what is also happening is that I have a long wire. OK, you see this guy here?
We had one of our union folks stretch out along the floor here. We have a really long wire that connects to the Vo node, and there's also a long corresponding ground. So, this wire is a coaxial cable that is used for Ethernet and such like.
It's got a core that carries a signal, and around the core is shielding that is the ground. OK, so that goes a long way, and at the end, it is open.
OK, it's an open circuit at the end.
I haven't connected anything out there: open circuit.
So, you know, something's happening here that's making the circuit behave like this.
So, this is VI. At Vo -- So at Vo I'm getting this funny behavior.
OK, so does anybody want to take the next piece of clues here, does anybody want to take a stab at guessing what might be going on here? Yes?
Ah, we have a shill in the audience here.
So, the theory is that the step here, think of it as an electromagnetic pulse that goes from zero to five, and things in real life don't travel instantaneously.
So, there's something with a wave that flies down, and the wave goes to the end, flips, and then comes back, and then establishes the full voltage here.
So that is indeed at the root of what's going on.
And let me put it in layman's terms and then describe the details of what's going on here. OK, so the way to view what's going on is that I have this long wire.
OK, in the very first lecture, I started off by saying wires are ideal. OK, ideal wires are such that I can transmit signals on them. Wires are small so that the propagation time of signals is inconsequential compared to the rise times and fall times of the signals of interest.
By having this really long cable here, I have clearly violated that assumption, which is the wires are really, really long here. OK, and so I somehow need to model what the wire is doing to my circuit when I don't have a small wire. So what actually happens, the way to view it is the following.
So, although this is a wire, to understand the mechanics of what's going on, I really have to model it much more accurately, OK?
And, the way to model a wire like this is that notice that every small element of a wire has associated with it some inductance. OK, so let's take a small segment of the coax cable here. The coax cable is a small core surrounded by a metallic shield. OK, that's a ground.
And so, when I have a wire surrounded by a metallic shield, that also has the capacitance, OK, inductance and capacitance.
So this small segment can be modeled as a really small inductance, and a really tiny capacitance.
Similarly, the next segment can be modeled as a tiny inductance and a capacitance. There is also a resistance here, but let's assume that the resistance is zero for our model, and also the parallel resistance is also infinity.
OK, so it's an inductor, capacitor, and really the situation that I have is not a pair of ideal wires, but really a really, really small inductance, and a small capacitance in parallel.
So, it's more of a set of distributed elements that I have here. Notice that in my lump circuit abstraction, when we talked about the RLC model for the wire between two inverters, we lumped it.
We lumped this thing into a model that looked like this.
OK, we lumped the resistance into a source resistance.
We lumped all the inductors into a lumped inductor.
We lumped all the capacitances into a lumped capacitance.
OK, but in this situation, I can do this when the signal speeds of interest are much, much, much slower than the speed of light than the propagation speeds of electromagnetic signals. In this case, that is not quite true. And so, therefore, we have to model it much more exactly.
We need to see what's going on. So, what's happening here is that at t=0, I get this step. So, think of that as a pulse of energy, and the instant it comes here, and instantaneously this guy looks like a voltage divider, OK?
I've chosen my resistance, R, here to match the instantaneous impedance looking in, which is also R.
I've arranged it to be that way.
So, instantaneously, the point at which the pulse appears at this point, looking down here looks like another resistor to this pulse. OK, therefore, when I start out, I start out going up and pausing at 2.5 because instantaneously, this looks like a resistance, R.
So instantaneously, it's a voltage divider, R, and so it's 2.5 here, instantaneously.
OK, then what happens? Then those little pulse propagates down. What does it mean for a pulse of energy to propagate down? Well, it begins sending a current through the inductor, begins charging up the capacitor, current here, so that's what I mean by saying that the pulse of energy goes down.
OK, it's a step that sends current to the inductor and charges of the capacitors, and that wave front moves out here and comes all the way here. What happens there?
Well, think about it. Supposing you stand here, and you hold a long string in your hand somehow, and just do this Gedanken experiment.
It's not easy to do. And so, let's say you somehow have the long string that you're holding onto, and the string on the other side is not connected to anything. OK, just imagine this experiment. OK, and what you do is you suddenly raise the string up at your end by about a foot.
What are you going to see happen?
So instantaneously, the string is up here, but the rest of the string is down a foot below.
And then you see this wave propagate down the string, right? So here's a string.
I lift this thing, and you see this wave propagate all the way down, the one foot wave propagate all the way down until you come here.
What happens here? So, out here, the string is down here, the wave propagates out here and pulls it up to one. And then what?
There's nothing connected there, so the string is zipped up, but it's got the energy. OK, where does energy go?
Well, it continues going up, and sends a wave back.
OK, so just think of a string that you pull up like this and propagates down, boom, hits the other end, reverses, and comes back at me. OK, you can look at a complementary situation, not the same as this, but complementary by taking a string, tying it to a door, and lifting it up. It's not the same situation.
It's a complementary situation where it's tied down.
Tying down a string is tantamount to shorting the ends here. OK, in that case what you'll see happen: as the wave goes down, at the end the string can't move, so the wave goes and flips around and comes back.
Try it out at home. Take a long piece of string, tie it up there, do this, OK?
And you'll see the wave go out, flip, and then come back at you. So, if your friends see you tying a long piece of string doing this, hopefully they won't think you're nuts or something. OK, so the same way here: this thing flies down, OK, there's no way to dissipate the energy here, so this thing continues up.
And then, what I'm going to see happen is the wave move back.
OK, the wave begins to move back, and that's another 2.5V, resulting in a net 5V at this terminal.
That wave begins to blast back, OK, and then when it comes back here, after some amount of time, it raises this to 5V, and that's what you see happen here.
So, this is a wave going down, and then after a time, 2t, it goes back up to 5V. That's a return wave.
It's 2t because to get down here is t seconds, and then t seconds to come back, which is why we have 2t.
OK, that is why you see that pulse at 2.5.
OK, so I'd like to show you a few more things here.
Clearly we don't want that in our circuits.
Could someone tell me what problem would happen if my signals looked like this in my digital circuits?
Instead of being nice little steps, if there was a little thing in the middle and then a step, what's the problem with signals like this? In digital circuits, what did it violate? Yeah?
Exactly. This little sucker here is meandering out in the forbidden region for all of 2T.
Can't do that. OK, can't have that.
Well, so we need to fix the problem because this is real life. OK, but what if you and your buddy were signaling each other but using digital signals from one dorm room to another maybe a few hundred feet down?
Your circuit isn't going to work because the signal's going to meander around in the forbidden region for some time.
So, any ideas what might you do?
Yeah? Put a resistor on the end.
OK, trick the circuit. So, what you can do, and I'm going to show you a little demo here, what you can do is the reason I got this wave propagating back, was that there was nothing to absorb the energy.
So instead, what if I put another resistor here, R? So, as far as a burst of energy is concerned, it says, oh, yeah, it just looks the same. It's R, and goes and dissipates in this resistor, R, and guess what?
I don't have any wave going back, and I'm done.
So, what I'm going to find, then, is that out here, this goes up to 5V, but out here, I will have a signal that starts out and goes up to 2.5, and that's it. OK, I lift it up, it goes down, it goes to 2.5 because in the lumped model that you've been dealing with, it's a resistor R, a resistor R to ground, and you're taking the connection here or here.
So, it's your standard lumped model, your voltage resistive divider, and it just simply works.
Yeah, that's it. So, this is the end of the cable. OK, if somehow you could watch this and that at the same time, so what I'm going to do, and this is a resistor, R, I'm just going to plug it in. OK, if the fates are smiling at me, what should you see there? What should happen is that the second jump from 2.5 to 5 should simply go away.
It should just go to 2.5. Let's try that.
There you go. I take it out, it jumps back up. OK, so all I've done here is put in a resistor at the end, and I'm still measuring the voltage here. So, that's one solution.
One solution is to put a resistor here.
So, I absorb the energy, and the resistance has to be equal to the instantaneous impedance looking in.
And the instantaneous impedance, for many of these cables is 50 ohms. It's called a characteristic impedance. OK, you'll learn a lot more about it if you take 6.014. That course starts out with assuming that things are distributed in that matter.
OK, so if you want to design multi-gigahertz chips, it turns out that if you have signals that are traveling around at edge speeds in the 0.1-1 nanosecond range, remember, light travels roughly one nanosecond a foot.
And if the signals are roughly of interest are 0.1 nanoseconds, then if the chips are one inch in size, right there, the propagation speed of a signal across a chip is 0.1 nanoseconds. OK, so today, we have to deal with these issues and try to figure out what to do about them. OK, so that's one solution that somebody pointed out. There is a second solution.
Anybody else have a second solution for me?
And then there's a third solution, too.
So it's OK. You can give me either the second or the third solution. It doesn't matter.
Anybody? You have two to choose from, come on. Yeah?
You can do that, yeah.
So we could define the problem away by saying this transition is such that my high is below So, once it goes above 2.5, who cares what it does?
That's a good point. That's solution number four, and that works. OK, so I still need two and three. Put a diode in there?
Yeah, I guess you could. If the diode had the same kind of impedance looking in, it kind of may work.
That's solution 4.2. I'm still waiting for solution two and three. Pardon?
Cut off the cable? Exactly.
So, the solution says, work on a different problem.
And that is solution number two.
OK, so the idea is, the root of all evil, this long wire, which is why I had this thing here. So instead, if I had short wires, then what will happen is if it's a very small wire, it'll look like this. And the wire's small enough.
I will see an itty-bitty thingamajig out there, but not a whole lot. By the way, the fun thing is that you can actually calculate the speed of light, the experiment I just showed you.
Can we put that up again? No, the big one.
So, in the experiment that I showed you, this distance was about 500 nanoseconds, OK?
This distance was 500 nanoseconds this time interval.
The length of this cable is about 500 feet, somewhere around 500 feet. So you can figure out the speed of light. What's the speed of light?
So, this is about 500 nanoseconds, and this cable is roughly 500 feet. What's the speed of light?
Roughly a foot per nanosecond. So, would you believe that in 6.002 we've figured out the speed of light from a simple experiment? All right, so let's do the next experiment now. Let's take out the long cable, and connect a short cable instead.
So, what I'm going to do is disconnect the long cable, and instead, connect a small cable.
It's still relatively long, but much shorter than the 500 foot cable. So what you should see happen now is that the little step should not be this big, but much, much smaller. So, take a look up there.
There you go. OK, so with this thingamajig, the little blip there is very small.
And of course, if I make it even smaller, then that can virtually vanish. OK, so that is solution number two. So, we've done one, two, four, 4.2. So, what's solution number three? One more solution.
Pardon? So, another solution we mentioned is we change this resistance.
and that will work, if I make this very, very low, then I'll get much closer to 5V here.
Yeah, that's a possibility. That's solution six I guess.
So what was solution number three?
And you all should be able to solve this.
You guys know the answer. OK, you folks should be able to solve this. Yes?
Ah, clock. So, what I can do is just as was pointed out, that I leveraged my abstraction by changing my VOH and VIH thresholds.
So that'll work. The alternative thing is to use a clock. A clock is a distinguished signal that I send around in my digital circuit, OK? So all I do is if I arrange it such that my clock doesn't happen in this vicinity, but rather, my clock happens late enough, then I'm going to sample and look at my signals only on the rising and falling edges of the clock, in which case I won't be looking at the signal, but the signal is doing weird things. OK, so a decent clock would also solve the problem. OK, any last minute questions before we go onto the next one? OK, the next problem that we're going to look at is titled the Double Dip.
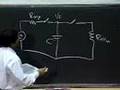
OK, so what I'm going to do here is our Vs power supply, and what I'm going to do is feed the power supply to an inverter. OK, so we've been doing this all along; Vs, I feed the supply to an inverter. And what I'm also going to do is, so this is ground, and I'm going to feed it to, so feed the power supply connection to a couple of inverters. OK, and what I'm going to do is apply some sort of a signal to this inverter, and I'm going to observe, and I'm going to look at this signal here. So, the abstraction should tell you that here's a power supply. This is 5V, or whatever the supply voltage is to these two inverters.
That should be fine, and feed some sort of input to this inverter, OK, and the output here should be simply determined by this input.
This signal can have absolutely no bearing on this output.
OK, and let's look at that and actually confirm it.
So, I build a circuit like this, and we look at this output, and initially there should not be any, it should simply work fine. OK, so it should work now, right? OK.
So what you have here, this input here is the input that I'm feeding to this inverter.
That is a straight line. Is that the power supply?
It doesn't matter? OK, so I believe this is the, we'll check in a few minutes, but I suspect this is the power supply, and this guy here is the output looking here.
So, the green one is the look here part.
So, there must have been a one-to-zero transition here, and that's all fine. So, so far, so good.
OK, no problem so far. Now what I'm going to do is I'm going to do something to the circuit that as far as abstraction is concerned, it doesn't show up on the circuit. OK, it's below the abstraction layer. OK, I'm going to do something, and suddenly, some things are going to happen. Look up there.
The circuit hasn't changed. It's the same circuit.
I've done nothing to the circuit.
OK, look at the green output. I've done nothing to the circuit that is visible here. OK, it's below the radar screen here. It's below the abstraction barrier. But, look at the disaster here.
OK, in particular, the spikes going up are not so much of a problem. Because of the static discipline, if I am at five or six or seven, it doesn't matter as long as I am higher than VOH.
So as long as I'm higher than VOH I don't have a problem.
But the problems are these repeated dips.
OK, the dips are a problem here, which is why I labeled this experiment the Double Dip. OK, the dips are bad because if they are large enough, they can then group the output down into the forbidden region, or worse yet, make it look like a zero. OK, so you're not prepared for this. So what I'm going to do is tell you what I did to the circuit, and then ask you to help me figure it out. So all I did was applied a load resistance to this, I think of 50 ohms or some RL.
I just applied a load resistor. And this inverter here, I believe, is a CMOS inverter that looks, OK?
So I have this input applied to this inverter, and all I did is I applied an RL load here.
And notice that the load here should not really change what's happening if this is an ideal inverter, OK, the load here should simply draw some current but really should not change any other property.
OK, so just remember, what's the signal doing?
The signal is high. This guy turns on, and current flows like this. So, let's say I had some sort of a capacitor here. This charges like this, and when it's slow, the PFET is on, and current flows through here down here.
And then when this goes high, this guy goes off, and this guy turns on. OK, so the current flows out this way and this charges through this guy.
When I turn it off, the P fret turns on and draws current from the top. OK, so do we have any theories as to why I'm getting that messy stuff, the dips and the spikes, on the output of this inverter? So why does this inverter care what the load of this inverter is?
I mean, who cares? So, put your thinking caps on.
Any theories? You guys did pretty well with the previous one. And this is much easier, actually. Need a better power supply; OK, so what I'm going to do is I'm going to replace the power supply, and instead, use a much bigger power supply at 5V. A big, mongo power supply that can supply 100 amps, and guess what, I've made the changes, but guess what, I still see the spikes. Good try, but it didn't work out. Good try, good try.
What next? Any other solutions?
Yes? So dips are because of the resistance, and the spikes are because of the inductance?
You're half correct. So, which one is it?
So, dips are because of resistances, and spikes are because of inductances. You're half correct.
It turns out that both the dips and the spikes are because of inductances. OK, but be that as it may, let me give you the next clue here, and then see if you can come closer to the answer. So, what I've done here is I've made this wire really, really long.
OK, it's a really long wire, OK, but it's a thick wire, so it's a long, long, thick wire.
So it's not the resistance. It's really, really thick and mongo, and it's a long wire, so a signal wire above a ground plane behaves like an inductor.
And so here, it has the capacitance to, but in this case it's inductance.
It's inductance here. So, I'll give you another ten seconds to think about it and then tell you the answer.
But despite the inductance here, it turns out if I take out this resistor, the problem goes away.
Look, I take out the resistor, the problem goes away.
Yes, there is an inductor here. OK, I take out this resistor, problem goes away. I put the resistor back in, boom. Yes?
OK, pretty good. That's 86 points.
So here's what's going on. There's an inductor here, and when I put a 50 ohm resistor here, I put this resistor. When the PFET turns on, it draws a current. OK, it's going to draw a current. It draws a current; remember that across an inductor, I have a drop.
And the drop relates to the di/dt.
Remember, for a capacitor, the current is Cdv/dt.
For the inductor, the voltage across the inductor is Ldi/dt. So, if di/dt, from switching a large current through the inductor every cycle, OK, big di/dt, di/dt is large.
I've made it large by having a very small RL, so, you know, pulling a big current through every few, whatever, every cycle, and then stopping it. And so therefore, I'm getting these big drops across this inductor that relate to Ldi/dt. In other words, the power supply here is fine. While you guys were watching, I switched to the huge, mongo power supply, and so this voltage is fine. But then this voltage after the wire is the problem. So, this voltage here doesn't look like this anymore. Rather, it has spikes that go down, for example, and when I switch the other way, they go up. OK, so therefore, what I end up having here is big spikes on this power supply.
And when this guy's power supply goes wacko, then I see the spikes on its output as well.
OK, so what are the solutions for that?
Any solutions here? What can I do to fix the problem? Pardon?
Stop using the, exactly.
When in doubt, do something else.
Build a different design. So what I could do is this is pretty dumb, using a long wire. And so, no, but trust me, oftentimes you go to the store room and they give you a big roll of wire, and you're too lazy to cut a piece out. Use the whole roll, and use the two ends, and connect it in, OK? So, if I had a much shorter piece of wire, then that can solve my problem.
But again, remember, what's small to you may not be small to the circuit. OK, so let's say, for example, I'm Intel, and I'm building a 10 GHz Pentium 6 processor. OK, it's 0.1 nanosecond is my cycle time. There, even a small, itty bitty wire can be a real problem.
OK, and so therefore, distributing power throughout a one inch chip that's clocking at 10 GHz is a really, really hard problem. And our own David Perreault, who is doing one of our sections, is one of the world's experts in this field. Distributing power, something as simple as, how do I get 1V in a stable manner to every single device on my chip?
It's a hard problem. OK, so now, you have to begin feeding your power supply connections much like RC circuits, OK, and you have to solve some hard problems to be able to simply distribute power decently throughout your circuit. So, what else can I do?
Yeah? Say it again?
Ah, I can do that. I could use different wires to connect each of the inverters. That's a good point.
So here, the coupling happens because I connect the two inverters way out here. So instead, I use a different cable. I hadn't thought of that.
That's a creative solution. OK, so in fact, if you build a chip, so we built this chip called RAW in our group, and it has on the order of 10 million gates. And this chip we built with IBM's technology, and it turns out that you don't send power supply in through a pin and then connect that 1.5V supply to all your gates. What you do is from that pin, you then build special power supply buffering trees.
And each tree, each leaf of the tree drives a subcircuit. In other words, if this is a chip, you have lots and lots of gates throughout your chip. What you do not do is bring in a power supply like this, and then connect.
You don't do that. That's the worst possible thing you can do. It's an absolute disaster for the reason just brought up. OK, so instead what you do is divide up the chip into, say, four quadrants.
OK, in our case, we have 16 quadrants.
And then what you do is from this point, you take one wire that goes to this quadrant, one wire that comes here, one here, and one here, so that you're getting the power supply very close to the source, and you have different connections going to each quadrant so that switching in this quadrant will not affect this guy because of the inductance of this lead here. OK, and if you hadn't taken 6.002, you'd have been arguing with IBM, I don't want 16 wires.
I want just one wire. OK, so there are other solutions, of course. There's a couple more solution.
One is that what you can do is part of the problem here is that all my transitions are really, really sharp.
OK, so di/dt is very, very large.
So, there's a whole new technique in design of digital and analog circuits, which talks about, maybe I should call it waveform engineering, OK, or edge engineering. OK, it's also called edge smoothing. The idea is that rather than have very sharp edges in your circuit, you try to have smoother edges. And when you have smoother edges, OK, then your di/dt is now going to be less.
It's not going to be very, very high.
Rather, your delta I is spread out over a longer period of time. Of course, that means the circuits may have to run a little slower, but that can also solve the problem.
And in fact, that same smoothing of the waveforms was also the solution you saw in the capacitive coupling we saw a month and a half ago.
And let me show you the demo, and then close up.
Not working? OK, that's OK.
It doesn't matter. So if you remember the demo from the lecture about a month and a half ago in capacitors, I talked about a chip with two pins, and there was this capacitive coupling between the pins.
And because of this, if this waveform is switching, then because of this coupling, you will end up getting, if this is the signal here, you will end up getting spikes on this pin because of the signaling of the other pin.
And that's good old capacitive coupling.
OK, and to eliminate this, what you can do is much like with the inductance system, if you, rather than having sharp transitions on this pin, if you have smooth transitions that look like this, then what you can do is you'll now spread delta V from here to here over a longer delta T.
OK, delta T has become longer, and because of that, you end up getting much better behavior, and you don't end up getting these spikes. So therefore, if you want to build really, really fast circuits, you have to be really careful. You can build fast circuits, but watch out for them fast edges.
OK, fast edges are nasty. They kill you.
That's something to remember as you build the next generation of circuits. Well, thank you all.
I had a blast, and I hope you guys had fun too. Thank you.
Free Downloads
Video
- iTunes U (MP4 - 127MB)
- Internet Archive (MP4 - 191MB)
Subtitle
- English - US (SRT)