Lecture 16: Sinusoidal Steady State

Related Resources

Lecture Notes (PDF)
Demonstration: First order sinusoidal steady state (PDF)
Demonstration: Displays the transfer function of RC lowpass and highpass (PDF)

• Download this transcript - PDF (English - US)

OK. Good morning.

Let's get going. As always, I will start with a review. And today we embark on another major milestone in our analysis of lumped circuits.

And it is called the "Sinusoidal Steady-state".

Again, I believe this will be the second and the last lecture for which I will be using view graphs.

And the idea here is that, just like in the last lecture, there is a bunch of mathematical grunge that needs to be gone through. And I want to show you a sequence in a little chart today that talks about the effort level in doing some problems based on time domain differential equations, as in the last lecture, something slightly different today and something much better on Thursday. And so, in some sense, Thursday's lecture and today's lecture involve talking about the foundations of the behavior of certain types of circuits.

And it is good for you to have this foundation as background, but when you actually go to solve circuits you don't quite use these methods. You use much easier techniques, which I will talk about next Thursday.

Let's start with a quick review, and then we will go into sinusoidal steady state. The last lecture we talked about this circuit and we did the same two lectures ago on Tuesday. We had one inverter driving another inverter. And we said that the wire over ground had some inductance. CGS is the capacitor of the gate and R is the resistance at the drain of the first inverter.

And if you look at this circuit, that circuit formed an RLC pattern. And what we did was we said let's drive this with a one to zero transition at the input.

And the one to zero transition at the input would cause this transistor to switch off, and this node would then go from a very low value to a high value.

So it as if a 5 volt step was applied at this input.

We also saw that using time domain differential equations that by applying a step input here the output looked like this. The output would show some oscillatory behavior when we have a capacitor and inductor.

I also gave you some insight as to why it oscillates like this.

And you also heard in recitation that the reason for this oscillation was because of these two storage elements.

Each of these storage elements tries to hold onto its state variable. For example, the capacitor tries to maintain its voltage while the inductor tries to maintain its current. And, much like a pendulum which oscillates back and forth, it swaps potential energy versus kinetic energy down here and swings back and forth.

In the same way, in an LC circuit like this, energy swaps back and forth between a potential energy and a kinetic energy equivalent, which swaps back and forth between energy stored in the inductor and energy stored in the capacitor and sloshes back and forth.

And because of this resistor the energy eventually dissipates and you end up getting a final value which corresponds to the 5 volts appearing here. And why is that?

That is because remember the capacitor is a long-term open for DC. It is a DC voltage.

After a long time this capacitor looks like an open circuit and the inductor looks like a complete short circuit, an ideal inductor as a complete short circuit for DC.

And so therefore in the long-term it is as if this guy is a short, this guy is an open, so 5 volts simply appears here.

And this is the transient behavior.

Then we just switch the first transistor off.

In the last lecture, I left off with intuitive analysis. Let me quickly cover that and redo the intuitive analysis for you.

I left it the last time by having you think about whether the transient response would begin by going down or begin by going up. And I will cover that today.

This was the circuit that we analyzed.

A VI input with a step and an RLC out here.

And we were plotting the capacitor voltage.

And intuitively we can plot this in the following way.

I have also marked for you the section number in the course notes which has a discussion of this intuitive analysis, (Section 13.8). Let's do the easy stuff first.

Notice that the capacitor wants to hold its voltage.

And so given that we don't have any infinite impulse here, I am going to start out with the capacitor voltage being where it is. And the initial conditions are given to you. You are given that the capacitor voltage starts out being positive at v zero and the current starts out being negative at time zero.

So I am telling you that there is a voltage v across the capacitor at time t=0 and there is a current that is flowing.

Since i is negative there is a current initially that is flowing in the opposite direction to this arrow here.

The i zero is negative. In light of that, I can start plotting my curve here by intuition.

I start by saying at time t=0 I am told that the initial voltage of the capacitor is at zero. This is about as simple as it gets. Completely intuitive.

I also know that after a long time, can someone tell me after a long time what the voltage will be at the end of the capacitor? You should be able to get his by observation? VI.

And why is it VI? It is vI because this is a DC value VI. And after a long time this guy behaves like an open circuit to DC.

This guy behaves like a short circuit to DC.

So since this is an open circuit, VI will appear here after a long time. And so therefore, after a long time, the capacitor voltage is going to be at VI. And I just showed you that.

There you go. You already have the two endpoints of your curve completely by observation, intuition. No DEs, no nothing.

Just by staring at it and understanding the fundamentals of how simple primitive circuit elements work.

Absolutely simple stuff. So you've nailed the two ends now and you cannot go wrong with the stuff in the middle.

Let's see. As a next step what I do is I need to understand what the dynamics of the circuit looks like here. What I do is I develop the characteristic equation. And initially you will write the differential equation and then substitute e^st and get this characteristic equation. But you could also remember it as a pattern. For a series RLC circuit you always get an equation of this form, always.

If this were R, L and C.

And whether you are looking at L up here or C up here, as long as you're looking at the capacitor voltage, the capacitor voltage is going to behave the same.

And for this circuit the characteristic equation remains the same as well for a series RLC.

It is exactly this. And I write the standard canonic form as s squared plus two alpha s + omega nought squared. And omega nought is simply one by square root of LC and alpha is simply R divided by L and I have two in the denominator as well.

And then I get omega d which is my damped frequency given by omega nought squared minus alpha squared.

And Q is simply called the quality factor.

And we will learn about Q in a lot more detail in about a couple of lectures from today. That is given where omega nought divided by two alpha. These parameters, alpha, omega nought, Q and omega d pretty much characterize everything else that I need to know about the circuit. First of all, omega d is the frequency of oscillation.

And so since omega d is a frequency of oscillation then I know that the time period of oscillation is two pi by omega d. Omega is in radians.

Notice that for typical values of circuits like this when R is pretty small, alpha squared is going to be very small. It's a common case for underdamped circuit that omega d will more or less be equal to omega nought. Commonly that is going to be the case. This frequency is governed by LC. And if R is large it is governed by this omega d here. So I have the frequency of oscillation. I also know that Q is related to the frequency of oscillation divided by alpha.

It is a ratio of the frequency divided by how badly I am being damped. So it is a fight between the frequency of oscillation and now heavily I damp.

And the ratio of that is an indication of how many cycles I ring. So Q tells me that the ringing stops approximately after Q cycles.

These four values, omega d, Q, alpha and omega nought are telling me more and more now.

So I have got these two factors.

So I know now, based on omega d and Q, that it is going to look something like this.

Some ringing here and then I stop at this point.

The last thing that is left to do here for me for now is to figure out whether I start out going down or I start out going up. I start out going down or I start out going up? I don't know that yet.

And I stopped at this point in the last lecture and let you think about how you can stare at the circuit and intuitively figure out whether this goes down or that goes up.

So here is the insight. Let's stare at this for a minute purely through intuition. The capacitor has a voltage v across it, right? And that is because I am telling you that it has an initial voltage v.

Now, I want to find out at prime t equals zero plus, in which direction does a capacitor voltage go?

Increase or decrease? What do I do?

Let me take a look at the inductor current.

I am told that the inductor current is negative which means I am told that the inductor current is going in this direction initially. The inductor current is pushing in this direction. Now, remember, just as the capacitor is one stubborn nut trying to hold its voltage, the inductor is as stubborn.

It is trying to hold its current.

It is trying to maintain its current.

And its initial current i(0) is in this direction.

Capacitor has a voltage here, that is v(0), and the inductor is yanking the current in that direction.

So what should happen to the capacitor voltage initially?

If I am at v(0) and someone is yanking current out, at least initially in that direction, what should the initial dynamics of the capacitor voltage look like?

Pardon? It should drop, which means that if the initial current is being pulled in that direction the capacitor voltage must droop to begin with.

Completely through intuition. No math here.

This means that i(0) is negative.

It is as if i(0) is being pulled out in this manner, so the capacitor voltage must drop to begin life.

Therefore, the dynamics look somewhat like this.

Notice that this is very reminiscent of the ringing that we saw at the gate node of the second inverter.

Let's stop here in terms of time domain analysis of RLC, and today let's take another big step forward.

Today marks another transition in life here.

This is actually a huge transition so I want to just pause and take like ten seconds of a breather just to clearly demarcate the fact that we have a huge transition coming up.

The key to this transition is that I want to look at today the steady-state response of networks to a sinusoidal drive.

We are going to do two things differently starting today on this new journey of ours. In the past, we looked at time domain behavior of circuits.

For RLC, for example, we looked at the transient response. And what happened the instant I turn something on? The transient response.

Today we are going to look at a steady-state response.

Steady-state response says that if I wait long enough, for whatever the circuit wants to do in the beginning of life to die out. If I wait long enough, how is the circuit going to behave after a long time?

I will tell you why that is important in a second.

I look at the steady-state behavior.

Second, I am going to look today at sinusoidal drive.

Two things that are different from, say for example, what I covered in the past ten minutes.

In the past ten minutes I covered two things which were different. One is that I looked at the transient response and then steady-state.

And remember for a DC input, for a DC voltage the steady-state was a DC voltage across the capacitor, correct? So the steady-state was pretty boring, it was steady-state DC. But what we are going to do today is instead of having DC inputs or step inputs which settle to a DC value after some time, we are going to drive a circuit through the sinusoidal input.

So you may ask me, Agarwal, are you nuts?

Why do you want to drive something with a sinusoidal input? Why not just steps in DC and so on? That was painful enough.

Why sinusoidal? Why not do triangular or why not do some other exponentially decaying stuff or something really cool like a whacko music signal?

What is special about sinusoidal stuff?

The key thing to realize is that, well, let me ask you a question first. How many people here know about Fourier series? Good.

It looks like some of you have taken the prerequisites.

Good. Need I say more as to why this is important? Just that question should give you the answer, right?

You've learned about Fourier series.

And when you learned about Fourier series you were wondering why on earth are we learning about Fourier series?

Who cares that you can represent the periodic signals as a summation of a series of sine waves?

Why is that interesting? Why are you telling me that I can take a square wave and represent that as a summation of periodic square waves and represent that as a summation of sines? Who cares that I can take a sequence of pulses with a fixed period and represent that as a sum of sines? Who cares that I can take a triangular wave and represent that as a sum of sines?

I am not sure what answer your math professors gave you when they taught you Fourier series. But in math they are purists.

They don't care about applications.

The answer could well have been because it is aesthetically pleasing. I mean isn't it cool that you can represent a sequence of pulses as a sum of sines?

That is good enough for mathematicians.

But I am an engineer. If it I cannot see how it helps humanity in the short-term then I probably don't care too much about it. Let me give you some practical significance of this. So it turns out that, since we know that we can represent periodic signals with sums of sines. What this means is that if I can figure out the behavior of networks to a sinusoidal input, if I can understand how to analyze a network for a sinusoidal input that means that if the circuit is linear I can then compute the response of the circuit to any periodic waveform. Here is the argument.

I can represent any periodic waveform as a sum of sines.

The Fourier series, remember?

If I just figure out the response of my network for a sine wave, then if this is a linear network, I can compute the response to any sequence of scaled sum of sines. A some sine, B sine two, omega whatever, C sine something or the other.

I can simply take the response of the one sine.

And from there I can go ahead, and knowing the response of a sine wave I can compute the response to a sum of sines.

That is pretty cool. Therefore, doing it for sinusoidal drives is really important.

Why steady-state now? Hopefully, I have convinced you that looking at the response of circuits to sinusoidal drive is important and interesting because we can long ways from there. What about steady-state?

Well, it turns out that, and I am going to show you, when you listen to music, you have an amplifier and listen to music, what you are observing by and large is the steady-state behavior of the amplifier.

You are listening to something over many seconds or many hours.

And the transients used for most of our common circuits, the transients die out pretty quickly.

And so the transients are quite complicated and they die out quickly. We say we are engineers.

Let's focus on what is practically important.

And we focus on the steady-state behavior as a large part of our analysis and just completely ignore the transient response when we care about the response to sinusoidal input.

The transient response will die away, and I will show that mathematically to you in a few seconds.

And let's focus on the steady-state because that what I am going to hear most of the time.

I am going to listen to an average over long periods of time. That's the motivation behind this. And let me put this in perspective for you. By now this should bring memories to your mind. This is the playground that we are in. This is the lumped circuit playground here. Remember we came from the playground of nature to the playground of EECS where we made the big leap from Maxwell's equations to lumped circuits, that's lumped circuit abstraction.

And within there we spent a large part of the last couple of months doing linear circuits. We also analyzed nonlinear circuits. Remember the amplifier circuit of the MOSFET large signal analysis was nonlinear?

Well, there is linear and nonlinear.

Within linear we also showed that if you take a digital circuit, at least as we understood them, and draw the subcircuit for a given set of switch settings, if I set the switches in a given way what I was left with was another linear circuit for a given value of all the switch settings. My small signal analysis was also linear. If I focused on small signals I also had linear analysis. Today what we are going to do is this. We are going to articulate a different part of the playground.

This was a big linear playground.

We've done this. We've done this.

We are going to explore this territory.

This is that territory of the playground in which we have sinusoidal inputs to circuits. Furthermore, we are going to look at a subcircuit of that region which is steady-state. We will look at sinusoidal input and in the steady-state. So that is going to be our focus for the next two or three lectures just to give you a perspective of where we are. To motivate this, what I would like to do is consider your amplifier.

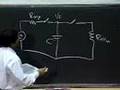
This is our friend the amplifier circuit, this part here. And remember, even though this is an amplifier, I am using a MOSFET here. And a MOSFET, as you know, has this gate capacitance CGS.

I am explicitly drawing it out for you here.

And I am going to drive this with a bias voltage plus some small signal vI, the usual template for amplifiers. And there is some Thevenin resistance attached to that source.

I am going to model my source as a bias voltage, a small signal plus some source resistance.

And I want to apply a sine wave here and I am going to look at what this looks like. You may think, look, this is a linear amplifier.

And so if I apply a sine wave here I should see some response here, and that should be the same amplitude if I feed the same amplitude here over any frequency.

But let's see what happens. Keep a look at, switch over to that view graph while I show you a little demonstration here. What you see here are three sine waves, a yellow sine wave which is the input here, you see a green sine wave which is the input vC at the gate of the MOSFET, and then you see the blue which is the output here.

For now simply focus on the yellow and the blue.

The yellow is the input and the blue is the output.

So I apply some input and I get an output that looks more or less some linear function of this input here.

It is a small signal. What I am going to do is I am going to change the frequency of the input.

Remember, I want to look at the response of the circuit to a sinusoid. I am feeding a sinusoid here.

I look at the response. I am going to change the frequency. That is a big shift that we are making in that the curve that we drew in the last lecture had to do with varying time. Now I am going to focus on sinusoids and vary their frequency.

I am going to change the frequency.

Stare at the blue curve as I increase the frequency and just think of what you might expect. Based on the knowledge you have so far you would expect that look, as I change the frequency, the frequency should change but I should see the same amplitude.

OK but take a look. Let me increase the frequency of the input. What do you see at the output?

I am increasing the frequency.

What do you see happening there?

If you don't see anything changing there you will need to see an optometrist. What do we see here?

As I changed the frequency, as I increased the frequency what happened to the blue? The blue kept decreasing in amplitude. And you are saying whoa, what is happening here? We don't have the tools to deal with this. I expected that when I changed my frequency, my frequency here should change of course, but why is the amplitude changing?

What is happening here? That is weird.

I noticed that this amplitude became smaller because the amplitude of the green became smaller.

And remember the green was the voltage across the capacitor.

So this is your RC. And here is my input.

My input has the amplitude, which I am holding more or less constant. And notice that vC decreased in value as I increased my frequency.

Just hold that thought. As I increased the frequency of my input the amplitude of the output kept diminishing.

In other words, the gain of the system seemed to have decreased as I increased by frequency.

And today we will look at why that is so and how we can analyze that. The other thing that is not so obvious here is there is a phase shift.

What I am going to do is try to see if we can observe the phase shift here.

Notice here. What we have been used to is for the amplifier we get a complete inversion at the output. Inversion means a phase difference of 180 degrees for a sine wave, right?

This peak should have been here, but notice that there is a shifting of the peak. In other words, if the yellow was my input my output should have had its minimum when the input had its maximum.

But notice there is a shifting of the signal such that the output is a maximum, not quite at the point where the input is a minimum but a little bit after that.

Also weird. Not only has this little circuit here lost its gain somehow, but also it seems to have shifted the signal in phase.

That is weird. And today we will look at why that is so and try to understand the frequency behavior of this little subcomponent here. Notice that vC is exactly 180 out of phase with vO. So vO is faithfully an inverted amplified form of the input vC. However, vC itself should have been the same as vI but it looks quite different.

So let's understand why that is so.

The subcircuit to model is the subcircuit comprising the source, resistor and the capacitor.

And I am just showing that to you here.

I have a vI, a resistor and capacitor.

And I am going to understand how this behaves.

And it is a first order circuit, single capacitor.

My input is a vI cosine of omega t.

vI is a real number for t greater than zero.

And I am telling you that the capacitor voltage starts out being zero. And my vI is a sinusoid.

It's not a step this time. It's a sinusoid.

So vI is a sinusoid and I want to find out what vC looks like.

The behavior here tells me, I will give you the answer, that when I feed a sinusoidal input as the frequency increases, vC should be decreasing somehow and also be shifting in phase. Let's do the derivation for that and see what happens. To give you some insight as to how to go about analyzing this let me draw a little graph as to the effort level of doing this. To determine vC of t on the y-axis here is our effort. How hard do we have to work to solve this circuit for a sinusoidal input?

And on this graph, down here is easy and up here is pure agony. Sheer agony up here.

So it's the scale of effort level ranging from easy to complete agony. And this is the time axis.

And the time axis starts out at 11 o'clock, the early part of today's lecture, and ends at roughly 12, that is today's lecture and this is next lecture.

What I am going to show you today is a method that uses a usual differential equation approach, and this is going to be pure agony. If you thought last Thursday was agony watch today. This is going to be sheer, sheer, sheer hell. So I am going to grunge through that, and I think I will sort of give up halfway because it's just too painful even for me here.

Then what I am going to do is at the end of this lecture I am going to show you an approach that I give a cutesy name.

I call it the "sneaky approach".

We are going to sneak something in there it is going to be a lot easier. And then in the next lecture I am going to show you an even sneakier approach that is just going to be absolute bliss. So let's start here.

Indulge me as I go through the agony part.

I am going to blast through it because that is not of how we are going to do things, but you just need to know that that is agony. Let's do a usual differential equation approach. Steps one, two, three and four. Set up differential equation, find the particular solution, find the homogenous solution, add up the two and solve for the unknowns.

It's a mantra. The four-step manta.

Let's do it. Step one, write the DE.

That's easy. We have done this before the RC circuit. It's RC dvc/dt+vc=vI.

This is no different from what you got from what you got from your RC circuit with a step input, just that my input is VI cosine of omega t in this case. It is not just a DC voltage VI.

Stare at that. Enjoy it while the going is easy. It's like traversing rapids, and before you come to a class five, you have calm and raging waters there, you kind of sit there saying oh, the scenery around here looks really good and so on.

All you are doing is stalling before you have dive down to class five. We will get to class five rapids in a few seconds here, so just enjoy this.

RC dvc/dt+vC=vI. You've seen this before.

Nothing fancy. Good old stuff.

VI cosine of omega t. You want to hold onto your seatbelts? OK.

Let's find the particular solution to the cosine input.

Let's use our standard method. What I will do is just so, there is going to be so much crapola up there, so that I draw your attention to vP, which is what we are trying to get, I am just going to put a box around vP in red. If you see like all sorts of garbage appear, just look for the red square.

That is what we are trying to get at.

That's the equation. Let's try.

First try, A worked before. A constant value A worked before for DC inputs. Let's try that again.

If it worked then it may work now.

If I use A, a constant value, and I substitute it here, I get dA/dt goes to zero, vP is A, but on the right-hand side I have VI cosine omega t. So clearly A doesn't work.

Sorry. I struck out.

Well, cosine omega t here, let's try A cosine omega T as my particular solution. Things are getting a little harder now, a little more painful.

So substitute A cosine omega t here.

So I do get A cosine omega T for vP, but out here I get RCA sine omega t times omega times minus one.

So I have a sine and a cosine, and I have a cosine on the right-hand side. Sorry, it doesn't work.

Nope, doesn't work either. Well, let's try A cosine omega t plus phi. We are now embarking into the rapids here. You can begin feeling the pressure. Just to refresh your memories of sines and cosines. A is the amplitude of the cosine. Omega is the frequency.

Phi is the phase. Remember the signal I showed you earlier? If something happens to the amplitude of the sine, something happens to the phase.

A cosine omega t plus phi. Let me plug it in here and go by standard practice. Here is what I get.

I plug in A cosine omega t to this equation, and this is what I get. I differentiate it.

I get omega out minus sine, sine of negative d plus phi, A cosine omega t plus phi equals VI cosine omega t.

That might work. Now we get into the class six part of the class five. All class fives have a little bit of class six rapids. Remember, the rapids go up on an exponential scale so it like earthquakes.

What I do now is expand out sine omega t plus phi, blah, blah, blah, it goes on and on.

I could go on and on, but this is even tiring me.

This can be made to work, but I am not sure I want to put all of us through this trig nightmare here.

If I am really, really nasty I could give this to you as a homework assignment or something, but I am not that nasty so you won't see that.

But if I go down this path it will get me to the answer, but I would have to soon negotiate class six, class seven rapids to get to where I want.

So let me punt on it, let me start from scratch.

I am at step two, let me start from scratch.

Instead what I would like to do is let's get sneaky here.

Rather than negotiating the class five rapids, what we can say is ah-ha, we can take our canoes and jump onto shore and run down and then get back onto the river.

Let's do that. That is called the sneaky approach. So that all our friends who are behind us think we are negotiating the rapids, but what we are going to do is get sneaky and take the shore path. Let's get sneaky, just walk down the shore and see what is there.

I want to do something completely weird here.

I want to look at solving this equation through the shore method. S stands for shore or S stands for sneaky, whatever you want. What I am going to do is rather than trying to solve for VI cosine omega t.

I am going to say let's try a different input all together.

And you will understand why in a second.

It's like I am the captain of my canoe and I tell my teammates, hey, let's not negotiate the rapids, let's go and explore the shore. Maybe down the shore we can find a path that gets us across to the other side more easily.

So here is me and my colleagues carrying our canoe and getting onto shore and taking a sneaky path.

This is not what I set out to solve.

I don't know where this will lead me.

But let's see where the shore path leads us.

I want to try solving this equation Vie^st.

S stands for shore or sneaky or whatever you want.

I don't know where I am going, but let's see where this leads us. Let's explore.

Make believe you are Columbus or something.

I don't know. Let's use the usual techniques and see how this works out. Let's try a particular solution, Vpe^st. My input is Vie^st.

I am trying to solve the circuit for a different input.

And let me try solution Vpe^st and see if that works out nicely. I substitute Vpe^st into my equation here, so RCVpe^st blah blah blah.

What I get here is Vie^st, Vpe^st stays the same, but here vP comes out, s comes out and e^st stays the same. That is nice property of exponentials. This is what I get.

A really cool property of exponentials is that when I differentiate it I get the exponential back.

Unlike a cosine I got a sine, and for a sine I got a cosine.

Exponentials are very plain and simple, are straightforward.

What you see is what you get. You differentiate it.

You get the same thing, you get scaling vP, S and so on, and some scaling here.

You get S scaling here, but the basic form stays the same. This is quite nice.

I have e^st in all three places, so I can cancel those out and I get this expression. And I get this.

Wow. So if I go down the shore I get some place fast. I don't know where I am yet, but whatever I did, it was easy.

I am just exploring this path, down the shore path.

I am making progress. I don't know where I have gotten yet. We will see where we got to in a second, but I got some place quickly, fast.

I was able to solve for this input Vie^st and get this solution very quickly. So what happened here?

I assumed the solution of the form Vpe^st, substituted it back, and found that if vP were equal to Vi/(1+sRC) then Vpe^st is a solution. What I have done here is that Vi/(1+sRC) is a particular solution to this equation for the input Vie^st. I put a box around it because this is important. This was easy.

We went down the shore, and said let's try this other input. We made rapid progress on shore and I got some place. I don't know where I am yet.

I got this. Let me pause here and let me give you the final answer. I am going to show you over the next five minutes that this is our answer.

You are staring at the answer already.

I am a party, I have taken a shore path and we have gotten some place. We see the river there, so it turns out we are exactly where we want to be, just after the rapids. All I have to do now is get my colleagues into the river with myself in the canoe and we are done. You don't know that yet.

My colleagues and I are sitting on the shore looking at the river. We've gotten some place.

There are no rapids there. We have gotten some place.

We don't quite know is this just after the rapids or not.

We don't know yet, but I got there very quickly.

And I will tell you right now, that is the place we wanted to go to. The next five view graphs I am going to blast through. There is going to be more pain and agony to show you why that is the case.

It's me thinking I am Columbus and proving to my colleagues that this is where we want to be.

And pulling out my sextant, and the compasses and so on that cartographers and people use to prove to my colleagues that this is where I want to be. This is the answer.

The next five view graphs will be demonstrating that this is indeed the answer, or close enough to the answer that we will be satisfied. Isn't this spectacular?

I am going to show you in about five minutes that this gives us all the information we need to know to compute the sinusoidal steady-state response to this differential equation.

Let me write that down here just so you know.

Just so you remember. I am going to put a marker on the shore that says this is where we are right now.

Now let me prove to you. As I just said, vPS is Vi, it's this stuff here multiplied by e^st is the solution to Vie^st. This guy here is a solution for Vie^st and vP is simply the coefficient that multiplies e^st. Similarly, if I substitute S equals j omega. I told you five view graphs of more hell, but I am just going to prove to you that this is it.

I am substituting S equals j omega.

This is Columbus giving a big speech at the end convincing his colleagues that we are where we want to be.

I substitute j omega for S and this is what I get.

This is a solution for e to the st, and so this is a solution for e to the j omega t. And let me mark this for you as something to remember. Vi/(1+j omega RC).

In terms of that, I am substituting j omega for S. And this is a complex number.

It is a complex amplitude. It is a complex number because of j here, and it multiplies e to the j omega t.

Just keep this in mind. So that was easy.

The steps were easy. I am still proving to you that this is where we want to be. Now let me draw the connection back to vP. And the first fact was that finding the response to Vie^(j omega t) was easy.

We know that. Second was the following observation that Vi cosine omega t is simply the real part of this number here. So Vi cosine omega t is simply the real part of Vie^(j omega t) from the Euler relation.

So cosine omega t is simply the real part of this guy.

Light bulbs beginning to go off?

The first fast was that finding the response to Vie^(j omega t) was easy. And the response was this, right? Times e to the j omega t.

That was easy. All right.

And the second part is that the real part of this is Vi cosine omega t was our input. Draw the connection between two steps. Finding the response to Vie^(j omega t) was easy. The real part of that was the input we cared about. Are light bulbs going off?

Let me draw you a little picture here to show you what is happening. Response to vI is vP.

It's the particular response we are looking for.

Remember the red square? But we threw in a sneaky input vIS and we formed the response vPS to that.

This step was easy. This step was hard.

vI to vP was hard, trig nightmare, remember? But vIS to vPS was easy.

It was a simple Vpe^st thing. We also know that the real part of vIS is vI. The real part of this is simply vI. If you have a real circuit, if you have a real linear circuit, for a linear circuit, if the real part of this gives me vI then the real part of the solution should give me vP. So computing vPS was easy.

If I take the real part of this, I take the corresponding real part of this. This is sort of an inverse superposition argument. Superposition, I said, take the response for A, take the response for B, add them up and you get the response for A plus B.

Here what we are saying is that get the response to A plus B, or to A plus jB and the real part of the input will produce the response given by the real part of the output.

So this is an inverse superposition argument.

If it is a linear circuit, then if vI is the real part of this sneaky input then I find the response to the sneaky input and take its real part I should get vP.

Here I am, Columbus, staring down at the entrance to this part of the river. I just proved to my colleagues that all we have to do is take the real part of what we have.

We can just jump right back into the river and get back to vP. And what I am going to do next is just grind through the math and just show you that.

I will just blast through it. It is not important, but you have it in your notes. I am telling you that vP is simply the real part of the sneaky output.

And I take the real part of vP e to the j omega t.

And I take the real part. And just a bunch of math here.

I am just taking the real part and doing a bunch of complex math. Remember vP was given by this quantity here. And I take the real part and I end up with vP is simply this quantity multiplied by cosine omega t plus phi, where phi is given by is given by tan inverse of omega RC, and this is the coefficient multiplying the cosine. So by taking the sneaky path and then taking the real part of that output answer, I was able to very quickly get to where I wanted to be.

So from here to here it is only math.

Recall, that vP, the thing in the red was what we set out to find out, which was the particular response to VI cosine of omega t.

And remember that two grunge is all of this stuff.

I am going to blast through two or three more view graphs that just give you more insight and more math, nothing particular.

And remember to solve the equation we have to find a homogenous solution, too.

But recall that the homogenous solution for an RC circuit is of the form Ae^-t/RC. This means that as time becomes very large this part goes to zero.

As time becomes large in the steady state, remember I care about the steady state?

This goes to zero. I don't care about the homogenous solution. Isn't that fantastic?

Most the circuits we will deal with, except for purely oscillatory ones, the homogenous part dies away.

You have something like e to the -t whatever.

It just dies away. It's gone.

So the total solution has vH going away.

And what I end up with is just vP.

My total solution in the steady state is simply vP.

And A is given by this that we just calculated.

I just have a bunch more insight that I talk about that you can look through in your notes.

And I just want to show you a very quick summary.

In summary, what we have is we computed vP.

It was a complex coefficient. And all these steps, 2 grunge, 3 and 4 were a waste of time.

And what I showed you was that for the input VI the coefficient vP was complex. And I can take the ratio and represent it in this manner as well.

And from vP, I can then compute the multiplier for the cosine as follows.

I divide by vP here. Remember the cosine was multiplied by, in the mathematical step that I did, VI divided one plus, this stuff here, so I could get the magnitude and phase of the transfer function of this circuit in the following manner.

And to wrap up very quickly, I am going to cover this again the next time and show you a magnitude plot.

Notice here that if I plot Vp/Vi.

Remember this was Vp here. That's the answer.

The magnitude looks like this. On a log scale Vp/Vi for small frequencies omega is at one, but as omega increases Vp/Vi keeps decreasing. That is the output.

Remember Vp was the amplitude of the output?

That keeps decreasing. And this is the reason why.

As I increase the frequency, the amplitude of my output cosine kept decreasing. I could also plot the phase for you. And the phase, in the same manner as omega increased, my phase also kept shifting from zero initially to pi/2 finally.

Let me stop here and start with this the next time and revisit this. Unfortunately, I won't have time for the demo. I will show it to you next time.

Free Downloads

Video

• iTunes U (MP4 - 87MB)
• Internet Archive (MP4 - 215MB)

Subtitle

• English - US (SRT)