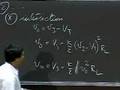Flash and JavaScript are required for this feature.
Download the video from iTunes U or the Internet Archive.
Topics covered: Energy, CMOS
Instructor: Prof. Anant Agarwal
Lecture 23: Energy, CMOS
Related Resources
Lecture Notes (PDF)
Demonstration: Energy and power in RC network (PDF)
Demonstration: Energy and power in CMOS (PDF)
All right, let's get moving. Good morning.
Let me take a quick poll. So, how many of you have completed Lab 4. Completed Lab 4?
Wow, that's great. So, how many people have begun Lab 4? OK, well that's good.
I won't ask the last question. OK so, well I hope you're having fun with this lab. Lab 4 was designed to be almost like a mini-project. And, it sort of ties together a lot of the content of the entire course.
And, it's not unlike the kind of systems that people design in industry, in systems that go into a variety of devices like, say, for example, digital CD players and stuff like that. A lot of mixed signal stuff goes in. OK, so today, I'm going to continue with our discussion of energy and CMOS.
CMOS will be a new topic that I will introduce.
So, the last lecture, we spent a fair bit of time talking about energy, and how to compute the energy of our inverter. So, let me start from where I left off, and I've given you a couple of extra pages of notes today just to sort of tie it to the previous lecture.
Right now, I'm going to start off on page three.
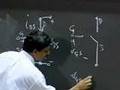
So, what we saw last time was an inverter of this sort, Vs, VIN, and we said, let's study the situation where this inverter was driving a load capacitor, C.
Where did this load capacitor come from?
Well, this inverter could be driving one, or two, or three, or four other larger gates, OK?
So, this C is lumped value of the gate capacitances of all of those inverters. This may also include some component due to wiring capacitance and stuff like that.
So, for an inverter like this, we showed in the last lecture that the formula for the average power was, so this was a static power independent of frequency, and this was called dynamic power, and it had some bearing, it's related to the frequency at which you clocked your circuit. So, this was related to standby power, and this to dynamic. So, what I also said is that I gave you a bunch of numbers so you could compute the power consumption of a chip that included 10^8 gates, 100 million gates, and at a frequency of 1 GHz, and a bunch of other numbers. C was given to be 0.1 femtofarads. Femto is 10^-15.
So, F was 10^9. VS was 5V, and for these numbers, if you plonk them down in something like this, for 10^8 gates on a chip, the average power would be 10^8 times these two. So, this would be five squared, which is 25, divided by twice.
RL was given to be 10 kilo-ohms, so, twice, 10^4. And here we had CVS^2.
So, C was 10^-16, 0.1 femtofarads.
Vs^2 was 25, and F was 10^9.
So, if you commence through the numbers here, what you end up getting is something that looks like this, 10^8 times this guy here. This is 1.25mW plus this guy ends up being 2.5 microwatts. So, this should come as a bit of a shocker. If I take 1.25mW, and multiply that out by 10^8, this says that each gate suffers a standby power loss of 1.25mW.
So times 10^8, I get 125kW, and this guy yields 250W. OK, the 250W is manageable.
It's still high, and just so you don't think that this is unreasonable, when the Pentium 4 first came out, it was consuming 170W of power.
OK, you should see the heat sinks on there.
There's actually a huge heat sink with a fan built into the top of the heat sink. OK, today it's down to more reasonable numbers like 100W and so on, but when it came out it was in this range. So it's high but not unreasonable. But this, of course, is totally wacko. OK, imagine carrying a laptop around, and the sucker is blowing 125kW.
That'll be fun. So, clearly there's something wrong here. What this is saying is that this gate here consumes 125kW, there are 10^8 of these on a single chip. OK, so we clearly have to do something about this, otherwise the semiconductor industry would fail. So, anybody have any ideas?
What do you think you might do here?
What do you think you might do to this inverter to make this look better, to bring it down? What can I do?
Anybody? Any ideas?
What do you think? Well, the problem is that if I look at this 125kW, well, there's a VS term here and an RL term here. So, I can increase RL.
OK, I can make RL four times or eight times as large.
That'll bring the power down somewhat.
Can anybody think of any problem with increasing RL?
If I make RL really, really large, will I run into other problems? Yes?
Exactly, the slowdown of the inverter.
Remember, the rise time of the inverter depends on how quickly I can charge this capacitor through RL.
So, if I make my RL really large, I will consume less standby power from hundreds of kilowatts to merely tens of kilowatts. But my gates will run as slow as molasses. So, clearly that's not a tradeoff I would like to make. So, I can reduce my voltage to maybe a volt. But that just reduces it by a factor of 25, VS squared.
So clearly, this is not going to work.
I have to somehow do something else, and that will be the topic of today's lecture. Also, I will dwell for a moment on this term. So, if you look at the spec sheet for the IBM's ASIC processor that we handed out, if you recall, we talked about power dissipation of 0.006 microwatts per MHz per gate.
OK, now you see where this is coming from.
Per MHz, that's because it's a multiple of f, the power. Second is that it's per gate, so this is the power per gate. So, as I have more gates, I just have that much more power dissipation.
It also says power supply voltage in the range of 0.7 to 1.3 right next to the power expression.
So, you can see why they tell you all of that, because both voltage, and the frequency, and the number of gates come into the power of equation.
OK, this really simple expression here, it's amazing how close this is to what people use for the dynamic power in chips. OK, so as the next step, what I'd like to do is, this guy, what do we do about that? OK, so we've taught you to build gates in a particular matter, but it's a non-starter.
So, how do we get rid of static power?
How do we get rid of static power?
OK, to do so, let's build up a little bit of intuition. OK, so the intuition goes as follows. So let's say I take my inverter. Let me draw the circuit both on the on state and in the off state.
So, when VIN is high, when VIN is high, I get the MOSFET turning on and has a resistance, RON, and Vo is the output voltage.
Similarly, when VIN is low, so when VIN was high, Vo was low because RON is much less than RL.
So, this voltage was low, while here, when VIN is low, the MOSFET is off, and so I have an open circuit out here. And because of that open circuit, the voltage here was going to be high because VS would simply appear there. So let's tailor this and see if we can build up some intuition as to what to do.
So, when VIN is low, I don't have any static power being dissipated because I don't have a connection from VS to ground. OK, the current, i, is zero. And, VS simply appears at the output. The reason this is so is have a switch here. So when this is low, the switch opens up and cuts the path from power to ground.
This is a nice situation. Here, when VIN was high, there was no switch that turns off.
Rather, I get a connection from VS to ground.
OK, so think about this situation here.
The insight here is, just imagine if I could do the following. Imagine if I could somehow magically elevate RL to be a very, very, very large number, if I could make this so high as to make the power really low only in the situation when the input was high, OK? So, imagine if I could do something like this. Imagine I could open circuit this guy, RON, so when VIN was high, if I could, instead of having an RL here, what if somehow I could make this RL become infinity?
OK, so in this case, output VO would be low.
OK, I get many benefits by doing this.
One benefit is that, look, I have opened this switch here so I don't have any standby current.
OK, the standby current is zero.
The second benefit is that my output gets dragged down to ground, OK? Out here, my output was VS multiplied by RON divided by the sum of these two.
Out here, I have a direct connection to ground, and nothing to the power supply, VS, and so therefore I have a nice, solid low. So the question is that, can I get this situation? OK, that is a key insight.
So, imagine that somehow, when this was high, I could get this to open up, much like when this was low, I got this to open up. OK, so think about it.
So, the intuition is that what I need instead of a resistor here, what if I have something like the MOSFET that I have here? So, I have a MOSFET here that turned off when VIN was low. OK, what if I did the complementary thing? What if I put in some kind of MOSFET here that would turn off when VIN was high?
OK, so, much like the MOSFET turned off when VIN was low down here, imagine if I could find a device that could turn off when VIN was high? OK, this would be on, but this would be off. So the behavior of this device would have to be complementary to this device.
So, we need some sort of a switch to introduce this new, little MOSFET device with slightly different properties, let me quickly review for you the properties of the MOSFET that we know about, so our N channel MOSFET, also called the NFET, this is what we've been seeing all this while, is drawn like this.
I have a gate; I have a drain; I have a source. And this guy is on when VGS is greater than or equal to VT, OK, and off when VGS is less than VT. You saw this before, OK, nothing new here. So, what I need is a device that behaves in a complementary manner.
OK, so the device is a P channel MOSFET.
By the way, I must point out, till about 1983-84 until the early '80s, that's exactly pretty much how chips were designed, OK, using an NFET for the switch looking down here, and a variety of different kinds of devices to be used as resistors.
OK, that's when technology began moving towards this new kind of technology I'm going to talk about, and that dramatically reducing the power consumed.
And, the P channel MOSFET was created, and this guy's called the PFET. It's a complementary device that looks as follows. OK, the difference here is that, to show this is complementary, I'll put a little circle here. It has a gate.
Just to make things a little clearer, flip the drain and source terminals, and this guy is on at a distinguished threshold voltage of this with the NFET device, let me put an N here to say that this is the VT for the N channel device. And for this guy, this guy came on when VGS was greater than some voltage.
So, VTN could be, for example, one volt. So, VGS was more than one.
This turned on. In this case, I wanted this to turn on when VGS is some value which is lower than, or much lower than, the source voltage.
OK, so this guy turns on when the gate voltage is higher.
This guy should turn on when the gate voltage is significantly lower than the source voltage, just the complementary behavior.
OK, so when VGS is less than or equal to VTP.
And in this case, the threshold voltage for the PMOS device, say, just as an example, maybe -1V. So this means that if the source is at, say, 5V, OK, then this device would turn on if the gate, for example, using that example was less than 4V.
So, this is five. If the gate fell below 4V, this guy would turn on. In this situation, remember, if this was at zero, the gate would have to be greater than 1V to turn on. In this situation, the gate has to be less than 4V if the source was at five to turn on. And, it's off.
OK, so this is a complementary device that I postulate that behaves in a complementary manner.
So, the gate voltage rises, this guy turns on, and in this situation, when the gate voltage drops below the source voltage, this guy turns on.
OK, so when there's a rising guy that turns on in this particular situation when it falls, the gate turns on and shows some resistance. In this case, the resistance would be RON. And to show that it's N channel, let me say N. And in this case, the resistance, when it turns on, would be RONp to represent P channel.
OK, so now consider the following circuit for the inverter. So, instead of my resistor, I put a complementary device, OK, and that's it.
So all I've done here is replace my resistor with a MOSFET that behaves complementary to the N channel MOSFET. So this is my gate, my drain. This is my source, my gate, my source, and my drain.
OK, and this guy is called a pull up, and this guy is called a pull down. OK, and the reason is that this guy pulls the output to ground when it's turned on, while this guy, when switched on, will pull this node up to VS. So, I pull it down or pull it up based on when the VIN is high or low.
So, let's look at the two situations.
So, let's say, as an example, my VS is 5V, and let's say VIN in one situation being 5V, and another situation being equal to 0V. Let's draw the equivalent circuit in both these cases. So, when VIN is high, I have my usual circuit. When VIN is high, this MOSFET, as before, when VIN is 5V, the N channel MOSFET below is turned on, and so I have an RON resistance here. But remember, VIN is 5, and VS is 5V, then the voltage across the source and the gate of this P channel FET is now equal, five and five. OK, so this one would turn off.
And that's the circuit that I get.
The output is suitably low. In this situation, if VIN is zero, what happens in this situation?
Here's my output. If VIN is 0V, the lower device turns off. This is zero.
This is zero. This guy turns off, and that's the situation for the N channel MOSFET.
How about this guy here? What happens here?
This is at 5. So let me just, this is at 5V. OK, and VIN is at 0V.
OK, so therefore, the GS of this is -5V.
If this is zero and this is five, G, source, and drain, GS is -5V, and -5V is significantly less than the threshold -1V in our example.
So, this one will switch on. And if this one switches on, what I end up getting is RONp out there.
So, when this one kicks in, it pulls the output high and VO goes high. So, all I've done is replaced my resistor with a complementary device, which switches off when the input is high, and switches on when the input is low. And the beauty of this is that at no point, assuming all the devices are ideal here, at no point do I have a short circuit between the output, do I have a current path from the output to the ground from the supply to ground, OK, I have this turned off or this turned off. So, this type of logic involving a PMOS transistor here, and the N channel transistor here is called CMOS logic for, OK, it's called complementary MOS logic.
That's what CMOS comes from. OK, so I'm sure you've read in a number of places that most digital chips today use CMOS technology. It comes from complementary MOS, and complementary comes from the use of complementary transistors: N channel, P channel, turns on when high, turns off when high, turns off when low, turns on when low. OK, that's exactly complementary to each other. OK, so what you've seen here has been the workhorse of the digital industry for the past two decades, 20 years, CMOS logic.
OK, and even the most advanced chip from Intel has an inverter that looks exactly like that. OK, if you count all the inverters in the universe today, I would say a significant fraction of those look exactly like that, no difference, just so simple. So, the key with something like that is there is no path from the power supply to the ground, and so by that model, I did not consume any standby power. OK, my standby power in that idealized model is zero. So, let's compute P.
So, what is P dynamic? Let's use the method that we adopted in the last lecture, and draw the equivalent circuit, and compute the power. OK, so I'm going to model the following situation, and assume that I drive a capacitive load, C.
OK, and as an input, as I did the last time, I'm going to assume I have some input voltage, VIN, that looks like this. The cycle time, T, and the frequency is 1/t, and let me assume that this is T1, and this is T2. OK, and I'm assuming that T1 and T2 are both much larger than the respective time constants.
OK, the time constants when, for discharging here, is C RONn, and here the relevant resistance is RONp.
The charging time constant is RONp times C.
OK, so T1 and T2 are assumed to be much greater than these two.
So when you look at this, there's one other benefit besides the power benefit, OK, of using CMOS logic compared to using NMOS. OK, it not only cuts out my standby power, but there is another significant advantage which is almost equal to the power advantage of this kind of CMOS technology.
Anybody have any ideas? What's the advantage?
What does intuition tell you? Is CMOS going to be faster or slower than NMOS? Why?
That's right. The key here is that the NMOS design I showed you earlier was relatively slow because it took me a while to charge up the load capacitor from RL.
In this situation, RL will become really, really small; it's RONp.
It's roughly the same magnitude as RONm.
OK, if so both of these on resistances are more or less equal and small, then the rise time will be of the same order of magnitude as the fall time, which makes this much faster than the NMOS.
In NMOS, my time constant was RLC, and RL was pretty large.
In this case it's RONp C, and RONp can be made to be very small because when it's switched off, the resistance here is infinity. So, in this situation, if I assume T1 and T2 are much larger than the respective time constants, I can go ahead and draw my equivalent circuit.
So, here's VS. So, for charging up, let's say this one is going to a one, or to a high.
So, I have VS going through a resistor, RONp, to a capacitor, and this thing is a switch.
So I have RONp, an ideal switch, going to a capacitor, C, this is my V out node, OK, so it's VS going through a resistance, RONp, an ideal switch, to a capacitor, C. That's a charging circuit.
For discharging, I have C, discharging through an ideal switch with RONn. So, this situation, I have an ideal switch, RONn.
OK, so that's the equivalent circuit for something like this.
So, in this circuit, during T1, this guy's off, and this guy's on, on during T1, and off otherwise. This guy is on during T2, and off otherwise. OK, so just imagine, this guy switches on, this guy switches off, this guy switches on, this guy switches off, OK? And remember, this is exactly the circuit I had analyzed last time in the last lecture, and the result given by v double asterisk. And that result was simply average power being CVS^2f. That's the exact circuit we used to compute the dynamic power, CVS^2f.
OK, so we're done. And how did this come about?
This came about because the intuition here is that I'm charging up the capacitor fully, and then I'm discharging the capacitor through this other side, OK, and I'm consuming power, dissipating power, in these two resistances during charge up and during the discharge.
Half the power gets consumed during charge up, and half during the discharge. So, I'd like to go back to doing a few numbers here, and taking a look at how, even with this expression, life can get pretty thorny as we go ahead into the next decade.
OK, so for our previous example, we assumed that 10^8 gates, F=1 GHz, C=0.1 femtofarads, VS was 5V, and I don't need RL anymore.
OK, why is it that I don't have any resistance component here?
I don't have it here because the power consumed by this circuit is independent of those resistances, provided T1 and T2 are long enough, are much longer than the two time constants, RONp C, and RONn C.
OK, so I don't have RL in my equation anymore.
I don't have any standby power. So, based on this calculation, the calculation I did up there showed that I had 2.5 microwatts per gate, and for 10^8 gates I had 250W for a chip with 10^8 gates. So, I'd like to dwell on this, if you can move over to page eight in your notes, here. Let me dwell on this for some time, and pontificate on a few things.
First of all, this number, as I said before, is high, but not a disaster.
OK, so you can't use this in laptops, but it's quite OK for a desktop or a server, and so on.
If you just go and put your ear to a pedestal computer, you'll always hear it making a sound, and that sound is because of a big fan that's inside it. And, if you have a big enough fan, 250W is not such a big deal.
But, this is certainly a real problem for mobile devices.
For a laptop, this is unthinkable.
OK, so we have to deal with this.
The second issue is the following, that it's 250W for 1GHz. Now, the fastest Pentium 4s that money can by today are, what, how many GHz?
What's the fastest Pentium 4 you can buy today?
What's that? Does anybody have a 4GHz Pentium 4 here? Oh, darn, you beat me.
Anybody have a 3? 3GHz?
A couple. So, I have a couple of 3GHz machines, and our lab has a whole ton of them.
So, if Intel comes out with 4GHz machines today, they've been going up by about 1GHz roughly every year for the past couple of years. And, within three or four years, you're going to see chips, microprocessors that are in the 5-10GHz range, OK, assuming that all other things stay equal, which of course they're not, but just to give you some insight here, if I clock these guys and build circuits that are ten times faster, I very soon go up to 2.5kW, again as I said, all things being equal which they're not.
But just to give you a sense, as I increase my frequency, so does the power consumed by the chip, OK?
So, I really have to do something here.
So, if I stare at this equation, CVS^2f, I want to increase f because people will buy computers if I have higher frequencies. And, Intel has managed to use its marketing campaigns to pretty much convince consumers that high frequencies are a good thing.
OK, and whether they really mean anything or not, that's a different issue. So, we've got this huge power for assuming 5V, OK, so it turns out that microprocessors, as they come out, newer and newer versions run at lower and lower voltages.
OK, they invent technologies that use lower and lower voltages, and go from VS 5V to, today, VS on the order of 1.5 to 1V, somewhere in that range. So the moment you do that, you get a 25x reduction in power.
OK, so in going from 2.5kW, you would now come down to something on the order of 100W, which is, again, much more reasonable, again, all other things being equal. It turns out that the capacitance of devices also changes as you go to smaller and smaller devices. And, 100W is also pretty high, and still not good enough for mobile computers.
So, there are many, many other tricks that people use to get even lower powers. One trick is to play games with the clock. OK, what you do is, let's say for example in some computation you are not going to be using your floating point unit.
Or let's say I'm going to be using your integer adder unit.
OK, so what you can do is you can turn off the clock to those devices so that those devices do not even switch when they're not working. OK, if I turn off the clock to a device, the device isn't even going to switch, it's just going to sit there in limbo without consuming any power. It's equivalent to turning off both transistors. If you turn off both the PMOS and NMOS somehow, OK, it's not consuming any power. And by doing that, you can further cut down the power.
So, if you can idle some of your function units, it's called idling a function unit, idle a function unit for, let's say, half the time. OK, you would cut down power by another factor of two. We can idle, then, 75% of the time, come down to 25W.
So, those are the classes of tricks that people play.
I'm going to stop here and allow the underground guide folks to do the survey. But, suffice it to say that the power discussion that I've gone through with you is a very high level discussion as to the real thing.
In real life, what actually happens is that there is a fair amount of standby power even for CMOS logic. It turns out that although I don't have a path from VS to ground for my two transistors, it turns out that there are many leakage currents.
OK, currents leak through all kinds of places through the drain of the inverter, and so on and so forth.
And so, there is some standby power.
So, let me show you a quick demo while, I guess, the review handouts are going around.
And this shows the temperature of my CMOS inverter, and as I increase the frequency, you can just watch the temperature go up, and hopefully we'll blow this transistor. So, I'm increasing the frequency as you can see on the side here, and higher frequency implies more power consumption, more temperature, OK, and hopefully you will see some smoke coming out of, OK, I think I blew the inverter.
So, the output is gone. So, it's at 110 degrees there, and that blew it. Sometimes we see smoke come out, but I guess today is not one of our lucky days.
OK, so let me stop here and have the underground guide folks go through the reviews.
Free Downloads
Video
- iTunes U (MP4 - 98MB)
- Internet Archive (MP4 - 165MB)
Subtitle
- English - US (SRT)