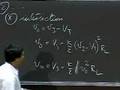Flash and JavaScript are required for this feature.
Download the video from iTunes U or the Internet Archive.
Topics covered: Op amps positive feedback
Instructor: Prof. Anant Agarwal

Lecture 21: Op Amps Positiv...
Related Resources
Lecture Notes (PDF)
Demonstration: Schmitt trigger (PDF)
Demonstration: Relaxation oscillator (PDF)
All right. Good morning, all.
You have two handouts, lecture notes and an article on mixed signal chips. A mixed signal stands for circuits that have both analog and digital components to them.
The reason I am giving you the handout is that Lab 4 and also your last homework involve designing and building a mixed signal circuit. It's a real fun exercise.
And I just wanted to tell you that from past experience people who have taken 6.002 often view the last lab as the single most fun thing they did in all of So, as you go into Lab 4, you should be telling yourself I should be having fun, I should be having, I should be having fun. You have to positively psych yourself. Otherwise, it's going to go by.
And then you're going to say boy, that was fun, I wish I had savored the moment as I was doing it.
All right. Let's see.
What do we do today? Today's lecture is actually going to be a fair amount of fun.
We are going to blast through a bunch of fun things.
And some things that you will be quite unprepared for.
Until now, in the last two lectures with op amps we talked about negative feedback. That is applying some portion of the output voltage to the negative input so that I could control this high strung device, my op amp.
Today, what we are going to do is try to get a handle on what happens if we use positive feedback.
It's the usual curious child. You tell them to do this, and of course they're going to try to do this as well.
And we are going to try to do that and see what happens and look to see if we can build some useful circuits.
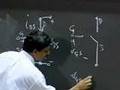
Today -- As motivation, let me do a quick review of a circuit that should now become affixed in your brains in a standard pattern. This is a circuit that gives you negative feedback.
R1 and R2.
And I apply a vIN. By now you should be able to look at this pattern. And this is your inverting amplifier pattern. So, you should be able to write down by inspection this is simply vIN or the minus vIN times R2 divided by R1. This is an amplifier whose gain is controlled by the ratio of R2 and R1.
This is a negative feedback circuit because it is always fun to do the intuition thing and say that look, if this voltage tends to go more positive than I care then this negative input goes more positive than I care.
If that goes more positive then the negative input v minus becomes more positive in the plus input which yanks the output down. So, there is a nice counteracting force that keeps the output stable.
Let's look at this circuit. Being curious engineers, let's look at the opposite here where I give myself some positive feedback in this op amp.
And it is going to be interesting to analyze this because what we find out on the face of it is not quite actually how it behaves. We are going to spend most of the lecture today on understanding the dynamics of circuits that look like this and to see if we can build some fun and interesting circuits and systems based on this kind of positive feedback. It is positive feedback because I am feeding back a portion of the output to the positive input. And you should be able to stare at this and already begin to intuit what should happen to this. Let's think about it.
This is zero. Remember, with positive feedback, the famous v plus is equal to v minus method doesn't apply anymore. Let's apply very simple analyses. If this is zero, let's say for example that this output tends to go a little bit more positive. This output, due to some noise or perturbation, tends to go up a little bit. If that goes up a little bit then because of feedback this node tends to go up a little bit. If this node tends to go up a little bit this exacerbates the positive input here and this one goes cachunk, whacks into the positive rail.
Let's take the other point of view and look at it intuitively.
What if this one tries to droop a little bit?
If it droops a little bit then the input at the plus terminal droops a little bit. If that tends to go down a little bit, that makes the output droop further and it goes and hits into the negative rail. I can see that this circuit wants to hammer into the positive rail or hammer into the negative rail because of the positive feedback.
It is like if you give incredibly positive feedback all the time, and by positive feedback I mean feedback encouraging the child to do whatever the child is doing.
It could be if he does bad stuff you give a lot of positive feedback or good stuff you give a lot of positive feedback then you are guaranteed to have a very good child or a very bad child. You are not going to have anybody in the middle. Same way here.
By giving positive feedback you're going to drive this into the positive rail or drive this into the negative rail.
Now, I am going to analyze this in two steps.
First I am going to analyze this using a method you've seen before which is replace the op amp with its equivalent circuit and analyze it statically. And by analyzing it statically we are going to show that the simple static analysis will yield the following expression. I put this in quotes, well, for a reason you will see shortly.
When I apply a plain and simple static analysis here is what I find. Let's go ahead with the analysis and see what is basically different about these two. And, first of all, I will confirm for you that our naive analysis we have seen so far will give rise to that expression.
So, let's go ahead and analyze that circuit.
And to analyze that circuit what I will do is replace the op amp with its equivalent circuit. If you remember the op amp is characterized by the following circuit, A times v+ minus v-, vOUT. This is the equivalent circuit of my op amp. And let me just impose that external circuit on this op amp. I have grounded my v- terminal.
My v+ terminal goes through a resistor and a supply, the v into ground, it's the resistance R1.
This terminal goes to the output through a resistor R2.
So, this is the equivalent circuit.
And I can apply the same good-old techniques I have learned about all through this course to this circuit and see what vOUT looks like. Very simply, vOUT is this expression here A times v+ minus v-.
And because of my ground connection v- is zero.
Then let me go ahead and replace v+ with the voltage that relates vOUT and vIN. What is v+?
v+ is simply the current through this part of the circuit, the current flowing here times the resistance R1.
That gives me the drop across R1.
And to that I add vIN and that will give me V+.
And then of course I multiply this by the gain here.
So, let me write down that expression.
The current through this is simply vOUT minus vIN.
That is the voltage drop between these two points.
I divide that by the resistance R1 plus R2.
That gives me the current flowing through here.
That times R1 is the drop across resistor R1.
And to that I add vIN and that gives me the voltage v+.
So, this is v+. That is simply vIN plus the drop across the resistance R1. Let me shuffle things around and put all the vOUT terms on this side here.
I get a 1+ for that vOUT and let me move AR1 divided by R1 plus R2 to the left-hand side. And I pick up a minus sign.
So, I get AR1 divide by R1 plus R2.
I pick up that. And on the left-hand sign I end up with vIN, and my vIN here is a function of the vIN that I have here. I have an A multiplying both the vINs. And then I get a one for this vIN here and there is a minus sign, so I get a minus R1 divided by R1+R2. That is the expression that I have. Let me go ahead and simplify that a little further and move this whole thing down here.
That gives me my expression as a function of vIN.
What I will do is, let me continue here.
vOUT=vIN A(1-R1/(R1+R2)). By the way, you may be wondering why I am going through so laboriously what is seemingly a very simple exercise. The reason I want to do is it I want to very carefully show you that the result produced by this exercise is exactly that. No magic here.
No cheating. We are going to get exactly that. And then stare at it and say huh, how did that happen? And then we are going to try to figure out how it actually behaves following that.
I divide this by 1-AR1/(R1+R2). And by now you should be familiar with the technique of ignoring small numbers when I have a big number next to it. So, AR1/(R1+R2) can be very much larger than one because A is very large.
So, I can ignore my one there. And then what I am going to do is multiply the numerator and denominator by R1+R2.
Oh, this A and this A is going to cancel out.
This A and this A will then cancel out.
And then I multiply the numerator and denominator by R1+R2, so this R1+R2 vanishes. I get R1+R2 here.
R1+R2 minus R1 is simply R2. And then down here I get a R1 and then I have a minus sign out there.
Notice that vOUT we have found to be equal to vIN R2 divided by R1. That is not wrong.
That is correct. Technically that is correct.
But you will see in a few seconds that in practice that that's rarely what you are going to see happen.
And we will try to understand why that is so.
What we have done so far, if you stare at these two panels here, first of all, we know that the inverting amplifier has the expression for vOUT up there.
And through this laborious exercise we have also shown that even with positive feedback, if I take a static view of the circuit -- If I take a snapshot of the circuit and simply analyze it as a static circuit, I get the same expression vOUT. But what we are going to do is when I explain to you that look, a small perturbation in vOUT is going to drive the op amp to the positive and negative rail, that is where the insight begins to show.
That if everything were magical and I could somehow exactly keep things just so that will be true.
I will be able to build that positive feedback circuit where the output is equal to R2/R1 vIN.
But remember even the slightly amount of perturbation is going to send the op amp scurrying off to the positive rail or the negative rail. How do we analyze that?
How do we analyze the behavior of a circuit that based on a small perturbation begins to move one place or another?
We want to analyze the dynamics of the op amp.
And to analyze the dynamics what I need to do is give you a slightly more detailed view of the operational amplifier.
If the operational amplifier is not moving instantaneously between the plus and minus rail, I need to give you a more detailed model that encapsulates the behavior of the op amp.
And so let me do that. If you want to study the dynamics of an op amp -- By dynamics I mean how an op amp moves as I perturb the input or the output and so on.
To capture the dynamics of the op amp we build a slightly more involved circuit, so v+ and v-.
This is what we've seen before, two terminals and dependent source that amplifies the difference input here by a large amount. Instead what we are going to do here is something slightly different and interpose the following circuit in the middle here.
This is a model of the dynamics of an op amp.
We are going to impose a small RC circuit in here.
This is R. This is C.
And I am going to call the voltage across the capacitor v*.
Notice what I have done is rather than say this is Av+ minus v- I am breaking it apart in two dependent sources, the first dependent source, which is simply v+ minus v-, and there is a RC time constant surrounding it and then here I simply add on my gain Av*. Notice that if it turned out that the resistance here, for example, was zero then v+ minus v- would appear across v* and this would be A(v+ - v-), what you have seen before.
It is always good to take a look at circuits and look at what happens when some component goes to an extreme value.
This would give you your basic op amp circuit.
What I would like to do next is analyze the following circuit to understand how positive and negative feedback work together.
And by understanding that then be able to explain how a positive feedback circuit works or a negative feedback circuit works. Here is what I will do.
This part simply corresponds to my positive feedback circuit, R2, R1. So, that is my positive feedback circuit. And I will do the same thing on this side.
All I am doing is applying both a positive feedback through R2 and R1 and negative feedback through R4 and R3 and representing the dynamics of the op amp and then standing back and ee, all right, let's see what happens to you.
So, I am sticking positive feedback, negative feedback, the dynamics of the op amp here and let's see what happens.
What I would like to do is impose this circuit on top of this op amp model. To save myself some effort, let me just go ahead and modify this circuit directly.
I get an R2 here, an R1 here, and then up here I get an R4, R3 here. The math is going to be just a little bit grubby but the result is actually pretty spectacular.
So, all I have done is replace the op amp with its internal circuit out here. And now we are going to take a look at what happens to op amp dynamics when there is a small perturbation. Let's develop an equation of this circuit containing a capacitor using techniques that we already know. Just to give you some insight into what you're going to see, notice that if I make a small perturbation in the voltage across the capacitor, let's say I make a small perturbation to the capacitor voltage let's say by applying some initial condition kind of thing onto the capacitor. Then let's say that the output changes to some value K. So, the change on the capacitor must have been K divided by A. And what you are going to see is what happens to the op amp when the initial condition on the capacitor is such that this output gets perturbed to the value K. Let's write an equation for this little circuit and see what happens.
Recall our goal was to understand what happens when I perturbed the output a little bit.
Here I perturbed the output such that its value goes to K.
And I can perturb the output by changing what happens at the capacitor. Let me write the equation for this circuit now and then to understand what happens to this capacitor circuit if I let go after giving it a small perturbation. What I am going to do is let me start by writing the good old equation for this little circuit here. And that equation is simply the voltage here v+ minus v- equals the voltage across the RC.
So, v+ minus v- will be equal to the voltage drop across the resistor plus that across the capacitor.
The voltage across the capacitor is v*.
The voltage across the resistor is the current through the capacitor C dv*/dt times R. So, v* plus RC dv/dt is equal to v+ minus v-. RC dv*/dt plus v* is v+ minus v-. You have done this millions of times before, but yet again.
This voltage here is equal to the drop across these two, and the drop across these two is v*, the drop across C, plus the current through the capacitor C dv/dt times the resistance R. Or you can apply the node method as well and get the same expression.
Now, we also know here that vO divided by A is v*.
I can go ahead and replace this guy here, v* by vO divided by A.
RC/A dvO/dt. Recall, I want the dynamics of vO so let me just get an expression in vO.
So, I get vO divided by A plus v+ minus v- equals.
Now, I want an expression in vO, an equation in vO, so I need to express v+ and v- in terms of vO.
What are these expressions? The expression for v- is vO and this voltage divider, so it's vOR3/(R3+R4).
And just for simplicity, let me call this some constant gamma minus. This is some fraction R3/(R3+R4). And let me call that fraction gamma minus. Similarly, v+ is vO R1/(R1+R2).
And let me call that gamma plus.
All I am doing is replacing v+ and v- in terms of vO.
So, effectively, what I have here is v+ is some fraction of vO. That's the best intuitive way of thinking about it, some fraction of vO.
And v- is some fraction of vO as well.
And I just stick these. I now have an expression in vO.
Don't get psyched by gamma plus and gamma minus.
Simply read this as if it is an F1 and F2 if you would like.
So, vO times some fraction minus vO times some other fraction. I am feeding back some fraction of the output to the positive and to the negative terminals.
Then, just moving things around a little bit, dividing throughout by A divided by RC.
So, I divided by A divided by RC.
Plus vO divided by RC. And what I am going to do here in a second, vO gamma plus minus gamma minus.
And I have multiplied by A divided by RC throughout.
Finally, collecting all the vO terms I get vO times one divided by RC plus A divided by RC. I got a plus sign here so I will just reverse these two guys in there, gamma minus minus gamma plus equals zero. All I have done here is simply grunged through some math to express this equation in terms of vO. And just to make it even simpler, I will just replace this thing by one divided by T, much as we did for first order equations.
What I end up with is dvO/dt+vO/T=0.
Despite all the grubbiness, I end up with something that is very, very familiar to all of us.
I went through a bunch of gyrations to substitute for v+, v- and v*, but at the end of the day I got the simple expression which was dvO/dt+vO/T=0.
Where capital T is the time constant of the circuit, and the time constant of the circuit relates to the expression in there 1/RC+A/RC(gamma minus - gamma plus). The gamma minus and gamma plus are the respective portions of the output fed back to the negative input and the positive input.
Now, as we all know, based on very simple intuition that we can completely predict the behavior of a first order of an RC circuit once we know what the initial condition of the capacitor is and once you know the time constant.
That's it. We know, we are masters at the fact that the capacitor is going to behave like this.
It is going to be exponential. And I do know that the time constant capital T. What's here?
It is simply the initial condition.
There is no drive input. I am not driving this with any input here. There is no input drive anywhere here. This is simply the natural dynamics of the system. And, recall, I start off with bumping the capacitor voltage such that the output starts off being K. That is it.
You should be able to write down this expression and the form of the response simply based on this.
So, this is what I bumped up the output to be by perturbing the capacitor voltage. My output response based on this equation is going to look like that.
Let's try to understand what that means.
It is actually quite a lot of fun.
How do we plot that response? You all learned that the way to plot the response is plot the initial value, plot the final value, and go cachoock, right? It's pretty simple.
I am going to start at K. I know that.
I am going to start at K and I am going to go and find out what the steady state value is. Here is where the interesting stuff comes in. The final value on the capacitor depends a lot on whether T is positive or negative. In my RC circuits that I looked at what was T? In the very simple RC circuit we looked at what was capital T? What was the time constant?
RC. This was RC.
This was a positive quantity. When capital T is positive my output is going to look like this.
When T is positive. And T is positive when this expression is positive. And if A is so large that I can ignore the 1/RC term, if A is very, very large and I can ignore the left-hand term here then T is positive when gamma minus is greater than gamma plus.
So, when gamma minus is greater than gamma plus, I have a stable circuit, this is the good-old stuff we have seen before. Now things begin to make sense.
Intuitively, what am I saying here?
All the gammas and other pieces of crapola aside, what am I really saying here in English?
What I am saying here is that if the portion of the output fed to the negative input is greater than that fed to the positive input then I have net negative feedback.
I have net negative feedback. I am feeding the output back to both the positive and negative inputs.
And if my negative input has a stronger effect then I am going to see the op amp output decay down to a value that I expect which is going to be zero. Notice that since I am not applying any input here, I expect the stable point for this to be output going to zero. I don't have any input there.
Let's take a look at another situation.
What happens when the opposite is true?
What happens when gamma minus is less than gamma plus?
When I feedback more, what happens when I do this, when gamma plus is greater than gamma minus?
The opposite is true. This means that I am feeding back more to the positive input. A bigger proportion goes to the positive than the negative. What happens then?
Then what happens is capital T becomes negative.
We cannot see this happening on the RC circuit because capital T is equal to RC, but here we have a more complicated circuit and capital T can go negative.
If capital T goes negative then this whole thing in the exponent there goes positive. If that goes positive what should the output look like? It should take off into never-never land. There we go.
I start off at zero and a make a small perturbation, and the output should go as t divided by capital T.
The dynamics of this it goes berserk, so it is net positive feedback. This is called a stable situation. This is unstable.
What happens when capital T goes to infinity?
When capital T goes to infinity, spend five seconds thinking about what it means physically.
What does it mean for the time constant of an RC circuit to go to infinity? That means that your R and C are very, very, very large.
That means that circuit is going to be very, very sluggish. Think elephant.
A big time constant. I want to move a leg.
It takes a while to do that. Think big.
Big time constant. So, everything is going to happen really slowly. It's like moving in molasses.
Big time constant. Everything is going to happen really, really slowly. If gamma minus is greater than gamma plus with a huge time constant it is going to look like this. And the output is going to look like this. I make T even larger.
All right. It is going to like this.
I make these so large that T tends to zero, T tends to infinity in which case I get this situation.
The output goes dah. OK?
Very slow. Very lethargic.
Big time constant. T tends to infinity.
And so if this is stable, this is unstable, this is called corresponding neutral.
And there is a mechanical analog to all of this.
You can show that this situation is akin to let's say I had a physical well of the sort and I had a ball in there.
I let the ball go. Then the ball will come down here and settle down in a stable state.
Any small perturbation of the ball will get it to come down and settle down here. The unstable situation is this situation where I have a ball sitting up here where any small perturbation will get it to zip down to a positive rail or to a negative rail. So, this is an unstable equilibrium situation. And exactly the reason we got this analysis in the static situation is that this can happen. If I do this circuit here and don't perturb it then I could get the output sitting at zero, but the slightest perturbation, boom, it is going to fall down or go up. What about the neutral equilibrium state? That can be modeled like a table top and the ball is here. It doesn't matter where you go.
There you are. How many people saw the Buckaroo Bonzi thing? Possibly well before your time.
OK. I have this table here.
No matter what I do to it, it just goes and settles down where it is, and that is neutral equilibrium.
But what this gives you is a fun view of the dynamics of the operational amplifier as I make small perturbations to it.
And the even more interesting thing here is you have the tools based on your first order RC analysis to analyze the dynamics of a simple op amp circuit. OK, so much for theory.
Now let's get to some action here.
All right. Fine.
That is really pretty, good and so on, but what can you do for me? What good does this property do for me? What can I build?
What we will do is look at the op amp circuit and focus on the situation where I have net positive feedback.
In particular just look at this circuit with R1 and R2 and send both to infinity. So, I have no negative feedback and I ground this terminal here and take a look at what happens to a circuit with positive feedback and see if I can build some interesting circuits. What you are going to do is build on a circuit called the basic comparator.
What is that? If I have an op amp that looks like this, and remember a VS rail and minus VS supply there, this is v+, this is v-, I can build a very basic comparator by doing the following.
All the circuits I am going to show you are going to build on this basic little circuit. What I am going to do is consider applying an input to the v- terminal, applying some sort of an input and taking a look at how the output behaves. So, I apply some input vIN.
And if I just do that, if this is v+ minus v- here then I am going to get something that goes like this.
That is when this is positive here then this guy is going to go to the VS rail and this guy is going to go to the minus VS rail. In terms of the, if I plot the same thing, in terms of vIN, and this is vOUT, if I plot the thing in terms of vIN then notice that as vIN increases this guy should go to a negative rail. So, in terms of vIN it looks like this. What this says is that as the input becomes more and more positive applied to v- then the output goes to minus VS, and if the input becomes more and more negative then the output goes to VS.
This is what is called a very basic comparator circuit.
It compares the two inputs and goes up if the input is in one direction and goes to the other rail if the input is in the opposite direction. So supposing I feed this- I can plot this is a function of time. Let's say I plot vIN.
Let's say I feed some vIN here. Let me just call this.
I feed some vIN to this circuit here, then what do you expect the output to look like, the output wave form?
For all positive vINs the output is negative.
So, my output vO is going to be negative as long as vIN is positive. And when vIN becomes negative this one shoots up and behaves like this.
This is minus VS. That is plus VS.
This is my input vIN. Then this guy is going to be my output. As vIN is positive output slams to the negative rail. When vIN becomes negative the output slams to the positive rail.
So, that is quite nice. And so such a circuit is pretty useful to me. Let's say, for example, I want to build a little digital circuit that is fed ones and zeros. I can use a comparator to turn my vIN voltage into a sequence of ones and zeros.
When vIN is positive I produce a zero and when vIN is negative I produce a one. I can get this one, zero, one, zero sequence coming out corresponding to the values of vIN being greater or less than zero.
Now, one problem with something like this is that this circuit can be quite messy in the following situation.
Suppose I superimpose a small amount of noise in vIN.
In particular, let's say that I have some amount of noise on vIN. I get a bunch of noise sitting around here. What happens is that at this point where the value goes negative, I do bump up.
But when for a second I have my input going above zero again -- -- this output comes down again and out here it goes up again.
I get this nasty behavior at the point where the input is around zero. When the input is around zero, the input is meandering around zero because of noise, I get a huge amount of up and down glitches on the output.
That's not very nice. And we will do a little circuit that attempts to fix that little problem.
What we are going to do is use positive feedback.
And I am going to build you a circuit that shows that we can eliminate this for small noise on the input.
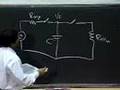
So, let's build the following circuit.
So I still feed vi to the negative input, but this time around I give it some positive feedback.
So, I give it some positive feedback.
And what I am going to do is feedback a portion of vO to the positive input. This is positive feedback.
And, in particular, let's assume that VS equals 12 volts. And to the negative one I connect -VS. This guy is going to go between 12 and -12. And correspondingly because these two are equal this one is going to go between 6 and -6.
This is going to be a 12 or -12.
Remember, the top rail and the bottom rail.
And this one is going to be a +6 or -6.
And let's understand how this circuit works when I apply an input vIN. Let's start by saying that assume my input is zero for a moment.
And let's say my output starts off being 12 volts.
The output is 12 volts then the input here is going to be 6 volts. In this case v+ is going to be 6 volts. The output is 12, v+ is going to be 6 volts. And my circuit is sitting out there doing nothing. Now, this started off being zero. Let's say vIN increases.
As vIN begins to increase what happens?
Well, nothing until vIN reaches 6 volts.
Since this is 6, vIN has to go up to 6 volts, has to equal this voltage before I can flip the circuit.
What happens when vIN is greater than 6 volts, if vIN goes above 6 then I have more voltage on a negative terminal than the positive so the op amp flips its state.
And vO gets to -12 volts. When vi goes above 6, vO gets to 12 volts. And what does v+ go to?
In this state v+ goes to half of -12 which is -6 volts.
Now, this guy is sitting at -6 and this guy is sitting at -12.
If this one keeps rising nothing happens, so output can stay at -12. So I am pretty safe.
Then let's say v begins to come down.
As v begins to come down, does anything happen when v gets to 6 again? If v is equal to 6 what happens? Nothing because this is at -6 now. So, there is still a huge net negative voltage here from v+ to v-.
And so therefore I sit at -12. Oh, well, I keep coming down until I reach -6. When I reach -6 here these two become equal. And what happens when this becomes less than -6? v- becomes less than -6.
If this one goes below this voltage, this is -6 and this is -7. There is a net positive voltage between v+ and v-, so this output swings to the positive rail like so. We will spend a lot more time on this in the next few minutes to really hammer the point home.
What is interesting about this is that even though the moment vi became more than 6, I swung to the positive rail, and then I had to go all the way back down to -6 before I could change state. I had to go way down before it could flip again. How can we make use of that?
Well, let me draw you a little vi versus vO diagram and then talk about how that can be useful to us.
This is vi, this is vO, this is zero.
Let's say this is 12, -12, -6, +6.
Let's plot that on the screen and see what it looks like.
As I told you, the output was at 12 volts to begin with and my input was at zero.
So, my input kept increasing. When the input hit +6 what happened to my output? My output swung down to -12.
As the input kept increasing nothing happened.
This was step one, this was step two, step three. My input kept increasing and output stayed at -12 volts. Then what I said was well, let's bring the input down. So, my input began to go down, step four, became more and more negative.
Nothing happened until I reached -6.
When I reached -6 I swung positive, step five.
Again, one, two, three, four, five. I am going up here.
It came up here. And nothing happens until I reach -6, but at -6 boom, I switch to the positive rail.
And as I get more and more negative I stay there.
Then again, as I start increasing again, nothing happens until I reach +6.
Think of that as your seventh step.
What is spectacular about this is that I seem to have a circuit that now has some knowledge of where it came.
If it is coming from here it switches at +6, but if it is coming from here it switches at -6.
So, there seems to be sort of a lag in the behavior of the circuit or some memory property in the circuit.
This kind of behavior is called hysteresis.
The word comes from magnetic circuits where, or rather elements that you're trying to magnetize.
Where if you take a magnet and move it over a piece of metal it may leave some residual magnetism in it.
And, in the same way, that is called hysteresis.
Same way here. As the voltage increases it seems to leave some residual in the circuit so that it effects when it shifts. The good news with this is that now, if I take the same kind of noisy wave form that I had before and do this -- If this is vi then what is going to happen is for vO I am going to be negative at this point. Nothing happens here because I have to get to -6 or +6 before something happens.
Out here I get to -6 and I switch state and go up to +12.
And then this one comes up above -6 very slightly out there. Nothing happens because the next change will happen only when the input goes to +6.
So, if eventually the input gets to +6 and then I am going to change state again. It is actually a really cool property and something that is completely non-obvious.
In the last 30 seconds let me show you a quick demo.
And, based on this property of hysteresis, I have actually built a little circuit. Let me do that first.
Notice here that I am showing you the input on the X axis vi and vO on the Y axis. Notice how the output switches at +6 volts and switches at a -6 volts to +12 or -12.
That's the hysteresis property. And we can actually use this property to build a clock circuit, which is on page 9, build an oscillator that sits there and oscillates by itself.
And you will see details of that in recitation tomorrow.
Free Downloads
Video
- iTunes U (MP4 - 141MB)
- Internet Archive (MP4 - 211MB)
Subtitle
- English - US (SRT)