Socks And Shoes
Parker has two pairs of black shoes and three pairs of brown shoes. He also has three pairs of red socks, four pairs of brown socks and six pairs of black socks.
Now let's say that Parker chooses a pair of shoes at random and a pair of socks at random. We would like to know the probability of him choosing shoes and socks of the same color.
-
Identify the outcomes! An outcome is _____.
We care about the color of the shoes and socks, so an outcome is determined by the color of the shoes and the color of the socks. Therefore, the correct answer is a pair of colors. -
Identify the event of interest!
-
How many outcomes are there in total?
There are two possible colors for shoes and three possible for socks. Hence, the total is 2\(\cdot\)3=6. -
How many outcomes are there in the event of interest?
The outcomes of interest (highlighted in tree below) are the ones where the colors are either both brown or both black. There is one of each.
-
-
Assign outcome probabilities
Please answer in the form of decimals with four significant digits.
-
What is the probability of choosing black shoes?
There are 5 pairs of shoes in total, 3 brown and 2 black. Since Parker chooses the shoes at random, the probability of choosing black shoes is \(\frac{2}{5}\). -
What is the probability of choosing red socks?
There are 13 pairs of socks in total, 3 red, 4 brown, and 6 black. Since Parker chooses the socks at random, the probability of choosing red socks is \(\frac{3}{13}\).
-
-
Compute event probabilities!
Please answer in the form of decimals with four significant digits.
What is the probability that he chooses shoes and socks of the same color?
Using the four step method we construct a probability tree: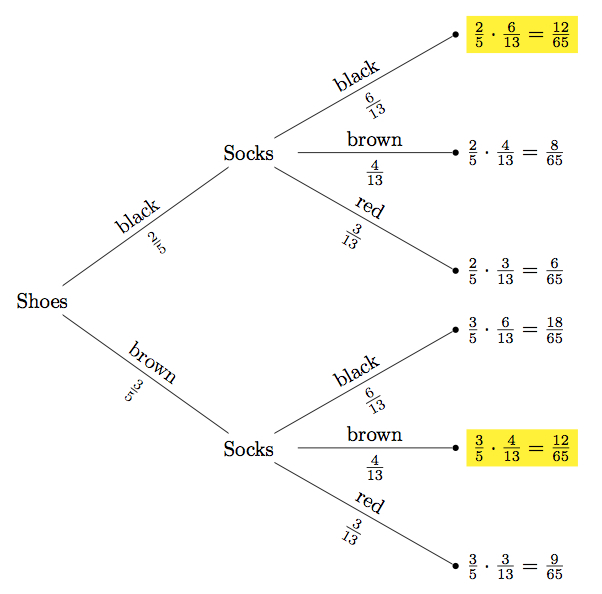
The probability of the event of interest is the sum of its outcomes. Therefore the probability that he chooses shoes and socks of the same color is: \(\frac{12}{65}+\frac{12}{65}=\frac{24}{65}\).
