Random Walks
Consider the following random-walk graphs:
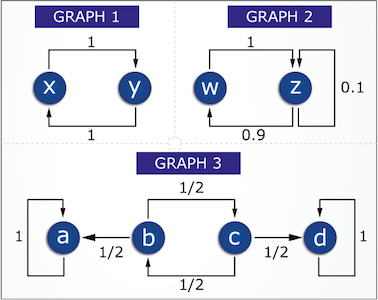
- Find \(d(x)\) for a stationary distribution for graph 1.
- Find \(d(y)\) for a stationary distribution for graph 1.
- Find \(d(z)\) for a stationary distribution for graph 2. Please answer in a fraction of the form x/y.
- If you start at node \(x\) in graph 1 and take a (long) random walk, does the distribution over nodes ever get close to the stationary distribution?
No, you will just alternate between nodes \(x\) and \(y\).
