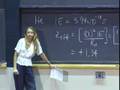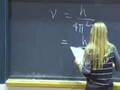Lecture 3: Wave-Particle Duality of Radiation and Matter

Related Resources

Wave-Particle Duality of Radiation and Matter (PDF)

• Download this transcript - PDF (English - US)

That is our proof that the The following content is provided by MIT OpenCourseWare under a Creative Commons license.

Additional information about our license and MIT OpenCourseWare in general is available at ocw.mit.edu.

Let's pick up from where we were on Friday.

We had discovered the nucleus. Now we were faced with the problem, as all the scientific community was in 1911, in trying to understand the structure of the atom.

Where was the nucleus in the atom?

Where was the electron? How were they bound?

How did they hang together? And we talked about the fact that the electron in the nucleus, the force of interaction is the Coulomb force.

And we started talking about how, at that time, the only equation of motion that was going to allow us to figure out how the electron and nucleus moved under influence of this Coulomb force was Newton's equations of motion, in particular the Second Law, F equals ma.

And so, in order to apply that equation of motion, we needed a model for the atom. And what was the simplest and most obvious thing to do was to suggest the planetary model.

After all, that is how the astronomical bodies moved around the sun. And so the model that is set up is one where this electron has a uniform circular motion around the nucleus with a well-defined radius, which we called r star.

We said that given this, the acceleration was a constant.

It was given by v squared over.

The linear velocity over r. We plugged that into F equals, put in the Coulomb force, and from that we were able to calculate the kinetic energy of that electron going around the nucleus.

Well, the reason I want to calculate the kinetic energy from this model is because I want to ultimately calculate the total energy. And why I want to calculate the total energy is going to be obvious in just a few minutes.

My goal is to get the total energy.

Actually, I am using my notes from Friday because I didn't finish them. You may need to get them out.

This will probably often be the case, is that I won't quite finish the notes from the other lecture.

I will start out the next lecture where I left off, so you should bring your previous day's notes to class if, in fact, you use them during class.

I want the kinetic energy plus the potential energy because I want both of them to add them up to get the total energy.

I know the kinetic energy. Now, we need the potential energy. What is the potential energy?

Well, the potential energy is the integral over the operating force over the appropriate limits.

In this case, if our force of interaction is the Coulomb force, which I will just represent as F of r, I am going to integrate this from r star out, and this is going to be minus the integral of the force. Now, some of you may have seen this before. This is a general case, the potential energy of anything is minus the integral of the operating force over the appropriate coordinates.

If you have seen it before, that is fine, you are happy. If you have not seen this before, you are panicked. Don't panic.

I do not hold you responsible for this.

You will see it in 8.01 later on this semester.

When you see it later on, you can come back here and say, okay, now I know what is going on.

But I just need it right now to make a point about the total energy of the system. And that is what is going to lead me to the conundrum. I need the potential energy.

It is the integral of the force.

Let me plug in, here, my force that is operating, e squared 4 pi epsilon nought r squared.

I do that integral and put in the appropriate limits. It is minus e squared over 4 pi epsilon nought r star.

Now I have kinetic energy plus potential energy.

Let me add them up. The kinetic is one-half e squared 4 pi epsilon nought r star.

Potential, minus e squared over 4 pi epsilon nought r star.

The result is minus one-half e squared 4 pi epsilon nought r star.

That is the total energy here of this particular system. Well, why I wanted this total energy is to show you that this total energy is negative.

What that negative means to us is that the system is bound.

The electron and the nucleus are stuck together.

And I can show you that maybe a little more clearly if I draw an energy level diagram. Let me plot here the total energy. And I am plotting it as a function of r, the distance between the electron and the nucleus. Well, what you can see is that for very large r, the energy here is going to be zero. Way out here, for very large r, where we have the electron and the nucleus separated infinitely apart, the energy is zero.

And, of course, as you bring them closer together, the energy goes down. And when you are exactly, and we calculated this, at r star here, well, then the total energy is minus one-half e squared over 4 pi epsilon nought times r star.

If you brought the electron and the nucleus into this value here of r star, the energy would change like that.

But the big point is this energy is negative, or it is lower than the electron and the nucleus separated. That means that the electron and nucleus are stuck together. You are going to have to put this much energy into the system in order to pull them apart.

That is the big point here, is that this model so far looks like everything is hunky-dory. Everything is working.

The electron stuck to the nucleus.

It is not going anywhere. It looks terrific.

But here comes the conundrum. The conundrum is that classical electromagnetism, which was pretty well understood by this time, 1911, 1912.

Maxwell's equations, that was down pat.

But what classical electromagnetism says is that when you have a charge, and this electron is a charge, that is accelerating, that charge has to be emitting radiation. It has to be giving off energy.

After all, that is actually how an antenna works.

In an antenna, what you are doing is taking charge and sloshing it, accelerating it.

When it accelerates, it emits radiation.

That is how you broadcast. That is true, it was known in 1911. Synchrotron radiation works the same way. When you have a synchrotron, the way you get synchrotron radiation is essentially by accelerating charge. That is a given and is actually, again, something you will talk about in much more detail in 8.02. But the point here is if this charge is being accelerated, and it is, then it must be giving off radiation. It must be giving off energy.

Well, if it is giving off energy, we look at our energy expression here. That must mean that the energy in the system is going down because it is losing the energy.

It is giving it off to radiation.

If E is going down, it is getting more negative here. The only way for E to get more negative is for this r star right here to be changing.

Is for r star to be getting smaller and smaller and smaller.

Well, we could set up another set of equations using what we know from classical electromagnetism and from what we have already done here. What we would find is that this value here of r star would go to zero in t equal 10^-10 seconds if r was originally on the order of an angstrom to begin with.

Here is the problem. Classical equations of motion coupled with classical electromagnetism, they are making a prediction that my atom is not going to live more than 10^-10 seconds. Because in 10^-10 seconds, that electron is on top of the nucleus.

We no longer have an atom that was already known to have a volume associated with a diameter that is about an angstrom. The classical way of thinking is making a prediction that is not consistent with the observations at that time. And even now, it is predicted that the atom essentially kind of annihilates, collapses in 10^-10 seconds. And that is the problem that the scientific community had in That is the problem we have right now.

And they had it for 10, 12 years.

Now you can say what is wrong here?

Well, it is possible, and they were thinking about this, too. It is possible that maybe this force is wrong, this Coulomb force.

That is a possibility. Or, of course, maybe it is the equations of motion that are wrong.

That is possible. Or, maybe it is classical electromagnetism that is wrong. Well, of course what it is going to turn out to be is the equations of motion, F equals ma. Bottom line is that you cannot use classical mechanics to explain the motion of this microscopic particle, the atom, in the constrained environment of an atom. That is the bottom line.

We need different mechanics. We cannot use classical mechanics to describe how that electron hangs on that nucleus, how they are bound. And so that was the problem.

This signaled something was really amiss in the scientific community in the world at that time.

That is our problem now, too.

What is the next step? Well, historically the clues about why the electron did not actually collapse into the nucleus, like classical physics predicted, came from a completely different area of discussion.

It came from the discussion of the wave-particle duality of light and matter. It was long believed that matter, with its particle-like behavior, was distinct from light, which was this transmission of energy through space. But, in the last 1800s and early 1900s, there were a few experiments that appeared on the horizon that began to suggest that maybe this boundary between matter with its particle-like behavior and radiation with its wave-like behavior was not as rigid as thought.

And, in fact, what we are going to see is that radiation has both wave-like properties and particle-like properties. It depends on the particular experiment that you do which one of those behaviors you see.

And, consequently, matter behaves both as a particle and a wave. Again, it depends on exactly what experiment you do, which one of those properties you observe. What we are going to do right now is put aside the discussion of the structure of the atom.

We are going to put it aside until next Monday.

We have to do that because we need some more information in order to take a big leap to get us out of this constraint of classical mechanics. And those clues, as I said, came from this discussion of the wave-particle duality of light and matter. And that is what we are going to be talking about for the next three lectures.

Then we are going to come back and tie in those results to the structure of the atom. Of course, where that is going to lead us is a new equation of motion called quantum mechanics.

That is where we are going. Let's start off by talking about radiation or light. We are going to talk about its wave-like properties, then Wednesday we are going to talk about the particle-like properties of light, and Friday we are going to talk about the wave-like properties of matter. That is where we are going.

Let's talk about waves here. You all know that waves are some periodic variation of a quantity.

A water wave, for example, is a periodic variation of the level of water.

At some points in space, the water level is high.

At other points, the water level is low.

Sound wave. Well, a sound wave is the periodic variation of the density of air.

At some points in space, the air is very dense.

At other points in space, the air is not dense.

Well, light or radiation is a period variation of an electric field, as I depict here on this slide.

Electric field versus position. There is a periodic variation of the electric field. Now, exactly what is an electric field? Some of you know this, some of you don't, but an electric field is literally the space through which the Coulomb force operates. For example, if we have a negatively charged plate and a positively charged plate here. The space through which the Coulomb force is operating here, and the Coulomb force is operating because we have two plates here that are oppositely charged. The electric field is the space through which the Coulomb force operates.

If we put a positive charge in that space, you know what is going to happen. In this coordinated system, the positive charge is going to float up.

Because the negatively charged plate is up above.

If we reversed the potential difference and put a positively charged particle in this electric field, in this space, it is going to move down because now the negatively charged plate is lower.

This electric field here has not only magnitude -- You can imagine here the magnitude is given by the difference in the potentials of these plates.

The larger the difference, the larger the magnitude.

But it also has direction. In one case, it is pointed this way. In the other case, it is pointed that way. And that is reflected here on this plot of the electric field here.

What you see is that right here, the magnitude of the electric field is small. As you move along in x, that magnitude increases, goes to a maximum, then turns around and at some point literally is zero.

And then the electric field changes direction and its magnitude increases in the opposite direction.

Increases, increases, gets to a point, then turns around and becomes zero again.

If you have a charge in a radiation field and you put it right here -- Well, it would be pulled in one direction. If you put it over here, it would be pulled in the other direction.

We have a magnitude and we have a direction.

Now, not only is light a periodic variation of the electric field in space, it is also a periodic variation of the electric field in time. That is, this is a picture of that field, that one instant in time.

We will call it t equals 0.

However, that electric field moves.

It propagates. And the distance, or the time it takes for the electric field here to move over one wavelength, I have shown this as a star.

The time it takes for this maximum to go from here to here, one wavelength, is defined as one period.

And a period is given by one over nu, where nu is the frequency of the radiation.

It is the number of cycles per second.

In other words, if you were sitting here at x equals 0, you were tied at x equals 0, and you were just watching this electric field come by.

You would see a maximum in that electric field, one maximum every second if the frequency is one Hertz.

In other words, the frequency is the number of maxima you would see pass by you per second.

Well, we have a unit to characterize frequency.

I call it cycles per second. It is cycles per second, but the formal unit is Hertz. Hertz is inverse seconds.

We leave out the number of cycles.

The number of cycles is implied in the unit of Hertz.

To give another example, here, suppose we had some radiation and the frequency of that radiation was one Hertz.

Suppose we had an electron, an electron is charged, and we put here at x equals 0 and we tie it at x equals 0.

What is going to happen to this electron?

Well, what is going to happen is that this electron is going to be pulled down and then it is going to be pushed back up once every second because the frequency, here, is one Hertz. It is charged, and we are tying it at x equals It is going to go like this. It is going to oscillate once every second if this frequency is one hertz.

Here it goes. An electron is pulled down and then pushed back up once every second.

Now, we, of course, can write an equation to describe this oscillation of the electric field in both space and time. x is the position variable, t, the time variable, and I have written it down here. I will explain this more in just a moment, but what I also want to point out is that an oscillating electric field always, always, always has perpendicular to it an oscillating magnetic field. That is well described by Maxwell's equations. Again, you are going to see that in 8.02. And the magnetic field here has the same essentially function form and characteristics as this electric field. And, because it does, I am just going to talk about the electric field.

Here is the expression for the magnetic field.

I just call it H. But, again, it is a function of position and time. Here is an illustration, just the variation of the electric field.

Light, radiation is actually a variation in space and time of both the electric and a magnetic field.

That is why it is electromagnetic radiation.

Now, let me show you on the 8.02 website.

Let me get that rolling. There it is.

Now we have to start it. All right.

One of these is the electric field.

The other one is the magnetic field.

This is a simulation that 8.02 has made for you.

You can go and look at it on the 8.02 website, but you can see it propagating here in time, and you can see its variation in space of this electromagnetic field. Let's look at this functional form just a little more carefully, just to make sure everybody is on the same page. I think many of you have seen this before. What we are going to do, because we have two variables, is we are going to hold one variable constant and plot it as a function of the other variable, just to explain the parameters that go into this functional form. At time t equals 0, if in this equation here I stick in t equals 0, I have a form that looks like this.

It is just the cosine function in x.

And you can see that the amplitude goes from positive A to minus A. And so what you see is that this A in front of the cosine, the physical meaning of it is just the maximum amplitude. If you were given a functional form with a number in front of a cosine, well, you could read off the amplitude immediately.

The other parameter that characterizes this wave is the wavelength. It is the distance between two successive maxima or two successive minima.

And you can also see here that the field is going to be at its maximum amplitude whenever this x is an integral multiple of the wavelength, lambda, 2 lambda, 3 lambda, or minus lambda, minus 2 lambda or zero.

If you were given a waveform and there was a number in front of the x, you can almost, by inspection, tell what the wavelength is. That number would be equal to 2 pi over lambda. Now what we are going to do is hold x constant and set it equal to zero, and then plot this functional form as a function of time.

Again, we have the cosine function, oscillates from plus A to minus A. Now the time between two successive maxima or minima is what we spoke earlier of as the period. It is the time for one cycle.

In other words, is it one over the frequency.

And you get the maxima then whenever the time is an integral multiple of the period, whenever time is 1 over nu, 2 over nu, 3 over nu, or minus 1 over nu, minus 2 over nu, or zero.

These are the characteristics of the functional form, amplitudes, wavelengths, frequencies. Now, I told you that the period was given by 1 over nu.

Let's just do a quick proof that the period is actually 1 over nu, one over frequency. How are we going to do that?

Well, what I said was the definition for a period was the time it takes the wave to move one wavelength.

If this is the wave at t equals 0, this then coming up here should be the wave at one period later.

And so, if we moved over exactly one cycle, what this means is that at one period later the functional form ought to look exactly like it did at t equals 0.

If I take my general expression for the waveform and plug in t equals 1 over nu, I get this.

What you can see at first glance is that it doesn't really look like this, or at least not just yet, but we are going to make it look like this and we are going to do so legally. What are we going do?

This just repeats that equation.

You can already see we have some cancellation here.

These two nu's go away, so I just have cosine ((2 pi x) over lambda minus 2 pi).

In order to simplify this, I am going to need a trigonometric identity, which you may or may not remember, cosine (alpha minus beta) is the cosine alpha times cosine beta plus the sine of the alpha sine beta.

I am going to let 2(pi)x be alpha, and beta will be 2pi.

I am going to plug that in. Here, we can see some nice simplification. This cosine 2pi, of course, is one. The sign of 2pi is zero, this term goes away, and what I have left is A cosine 2 pi x over lambda at t equals 1 over nu.

And, indeed, that is the same functional field as the field at t equals period is equal to 1 over nu.

Now, this wave also propagates in space.

It moves. It goes from here to here.

And another important characteristic of electromagnetic reaction is the speed with which it propagates.

Let's just quickly calculate what that speed is.

We have enough information to do that.

Speed is always distance traveled divided by time elapsed. And we said that at t equals 0, this is what our waveform looked like.

We also said that one period later, this is what our waveform looked like. We know at one period that the waveform moved over one wavelength.

The speed is the distance traveled, which is a wavelength, divided by the time elapsed, which is 1 over nu, the period. Therefore, the speed is lambda times nu. That is the speed with which this wave propagates. And, of course, you already know that all electromagnetic radiation has a constant speed of about 3x10^8 meters per second, or we call it c. And what that is, is the product of the wavelength times the frequency.

The electromagnetic spectrum, of course, is infinitely wide.

And here is the electromagnetic spectrum.

We won't do this in any kind of detail, but I just want you to note here that on the long wavelength end, we have what we call radio waves.

And on the short wavelength, then, we have our gamma rays and cosmic rays. And, in the case of the gamma and the cosmic rays, because the wavelength is small, lambda is small, that means those waves have a high frequency. In the case of the radio waves, because those wavelengths are long, that means those waves have a lower frequency because the frequency times the wavelength is a constant. It is this c.

It is 3x10^8 meters per second. And, of course, right in here, a very small region, narrow region of the electromagnetic spectrum, are the light waves that are sensitive to our eye.

What you do need to know is that the red wavelengths are longer and the blue wavelengths are shorter.

Again, the important thing is lambda times nu is always, for every kind of radiation, equal to a constant.

And that constant is c. Now, the other thing that you just need to know is the relative ordering here in wavelengths. You do need to know that microwaves are longer wavelengths than gamma rays.

All MIT students should know that.

And one other thing I might say, because we are going to talk about this a little later in the course.

See these microwaves? Well, molecules will absorb microwaves, take it in. That kind of radiation is going to set the molecule rotating. Molecules will absorb infrared radiation, and that kind of radiation is going to set the molecules vibrating. Molecules will absorb visible and ultraviolet radiation. What that is going to do is promote an electron to an excited state.

Then sometimes those electrons, in the excited state, want to relax back down to the ground state.

When they do so they give off radiation.

That is the origin of fluorescence and sometimes phosphorescence. Then sometimes molecules will also fluoresce if they absorb X-rays, but with X-rays, if a molecule absorbs them, it also kicks out an electron.

And we will be looking at that in a few days to identify the energy levels in atoms and molecules.

This, I think, you are familiar with.

So far I have just told you what electromagnetic radiation is, how we characterize it: speed, frequency, wavelength, maximum amplitude. But what I have not shown you, yet, is any evidence that indeed light has wave-like characteristics. And to do that we are going to do the experiment that essentially was done to demonstrate the wave-like behavior of light, and that is Young's two-slit experiment.

This is the late 1800s. What was done was to take a source of monochromatic radiation.

We are going to use 6 angstroms, 633 nanometers.

It is a helium neon laser. And it is going to impinge on just a thin metal plate. It does not have to be metal.

It can be anything. But what we did was poke two holes in it, made two slits. And naively you might think, if you looked at a screen out here, that this screen will light up in spots that are directly opposite those slights.

Because, after all, light travels in straight lines. And so if the slits here are 0.005 meters apart, you might think that the two bright spots on the slit will be about 0.02 inches apart.

Well, of course, that isn't the case.

What you really see is an array of bright spots.

And Christine has up there in the projection booth a helium neon laser that is shinning behind two slits.

You've got really beautifully now, Christine.

That is great. And what you see is that there is a whole array of spots. There aren't just two spots.

There is a bunch of spots here, bright spot, dark spot, bright spot, dark spot.

You've also got another pattern superimposed on that.

It almost looks like you would see the single slit diffraction, too, on top of the double slit, but we won't get into that.

But this is not just two spots. Let's see if we can try to understand how this pattern arises, what this pattern comes from. Well, waves have the property of superposition. Superposition means that if I take a wave and have it in space, but now I take a second wave and put it in the same place in space but make it such that the maxima of both waves are in the identical place in space, what I have is a situation where the two waves add that property of addition of waves -- When they are in the same place in space, that property is called superposition. That is the property of waves.

And in this particular case, we are going to have what we call constructive interference. They are going to add up such that the amplitude here of the resulting wave is going to be twice the amplitude of each of the individual waves.

This is constructive interference.

On the other hand, I can have two waves in the same place in space, but they can be positioned so that the maximum of one wave is at the same point in space as the minimum of the other. And because we have these positive and negative amplitudes, well, then these are going to cancel when they add up and we are going to have the null result. We are going to have no intensity. That is called destructive interference. Well, in order to understand how this property of interference gives rise to these array of bright spots in the two slit experiment, let me actually use water waves as an example to try to understand why we get this array of spots, or this row of bright spots and dark spots. Here is the beach.

Here is the water. This is the top view.

Here is the water. Here is the sand.

Here is where I wanted to be all weekend.

And the waves are rolling in to the shore.

There are the wave fronts. And then suppose I get ambitious and, for whatever perverse reason, I decide to build a barrier to prevent these waves from coming onto the beach. Except I poke two holes in the barrier, two little holes. Well, you know what is going to happen. When the wave approaches that barrier, well, through that little hole a little bit of the wave is going to sneak through.

And because that little hole is really pretty little, what is going to happen is that the wave front is going to spread out isotropically. And so that wave front is going to look like a semicircle centered on that little hole.

And, of course, this wave front is going to keep propagating. And it propagates out.

And then soon enough, a wavelength later, another wave sneaks through and I have two semi-circles.

And the distance between those two semi-circles is lambda.

That is the wavelength. That is the wave crest.

That is the maximum of the wave.

Keep going. That propagates out.

Keep going. That propagates out.

Well, at the same time that the waves are sneaking out through that little hole, waves are sneaking out through this little hole. And I will color them green.

That wave propagates out and keeps propagating.

The other one sneaks through and keeps propagating.

And now let me clean up the drawing a little bit.

And I am going to call this slit one.

The green waves are the waves that have come through slit one.

The blue waves are the ones that have come through slit two.

And the distance between any two successive maxima here, or any two semi-circles is, of course, lambda.

And lambda is the same for slit one and slit two.

Now, I want you to look at this spot that I just circled right here. Right here what do you see?

Interference. Absolutely.

You have two maxima at the same place in space.

You are going to have constructive interference right there. What about this spot?

Constructive interference. What about this spot?

Right. Everywhere along that line you are going to have constructive interference.

Now, let me just tell you one other thing.

We have every constructive interference all along this line. Now look right at this point here. What you see is you have the superposition of the blue wave that has come from slit two, and this blue wave has traveled out from slit two a distance four lambda. One, two, three, four lambda. That is the radius.

It has traveled out a distance four lambda.

It is constructively interfering with a wave coming from slit one that has traveled out a distance three lambda.

One, two, three. The difference in the distance traveled by those two waves that are constructively interfering is one lambda. Let's keep going in order to understand this diagram. Let's look at this spot.

Right here, what do you have? Constructive interference.

Right here you have constructive interference.

If you kept going you would see, everywhere along this line, constructive interference. Now let's look at the difference in the distance traveled by the waves that are constructively interfering along that line.

Well, you see the green wave here?

The wave that is constructively interfering is one that has traveled out a distance two lambda.

That is, r sub one is equal to two lambda.

It is interfering with this wave front that has traveled out a distance four lambda.

The difference in the distance traveled by those two waves is two lambda. 4 lambda minus 2 lambda equals 2 lambda. I think on your notes, it is actually this case that I have written it down.

Here is another point of constructive interference.

Here is another point of constructive interference.

Everywhere along this line, we have constructive interference. And, if you analyze this, the difference in the distance traveled would be zero.

What you would expect, if you were to image this, you'd expect right here very bright spot, very bright spot, very bright spot. This is going to be symmetric around the center, so there will be a bright spot out here, a bright spot out there.

Let's look at this actually in real life in a water tank.

There we go, up here on the side boards.

Here are the waves coming this way onto some barrier, and here are the holes. Here is one hole.

Here is the other hole. And then these bright semi-circles are the wave fronts.

And what I want you to notice, and you have to kind of look out here, right there you see a whole bunch of very bright spots. Well, if this were light and we had a screen then right here we would see the screen light up.

And then right here you see kind of nothing.

That nothing is destructive interference.

That would be a dark spot if, in fact, this were light and we were looking at a screen. Then here is another very bright spot. Here is another very bright spot. This is on a website from the University of Colorado, which, if you are not familiar with, is actually kind of a very neat website.

It has some very elementary topics in it, but it also has some topics that even you would be interested in. And that is actually the name of the website. And so what is going on here, in the case of the light, is just what we have explained.

We've got this line of constructive interference that is going to result on the screen as a very bright spot.

And then another line with another bright spot and another line with a very bright spot. And this is symmetric around the zero. Right at this point we have constructive interference. In between we have destructive interference. Constructive, destructive, constructive.

And that is the origin of the many different bright spots.

And now there is a condition that has to obtain in order for there to be maximum constructive interference, and that is this condition. The difference in the distance traveled of the two waves that are interfering to give us that maximum constructive interference has to be an integral multiple of the wavelength.

I will explain this a little bit more starting on Wednesday.

Okay. See you then.

Free Downloads

Video

• iTunes U (MP4 - 111MB)
• Internet Archive (MP4 - 197MB)

Audio

• Internet Archive (MP3 - 11MB)

Subtitle

• English - US (SRT)