Help   |   Contact Us

 

Lecture 12: Dispersion, Phase Velocity, & Group Velocity

OCW Scholar

« Previous | Next »

Lecture Topics

A graph written on a chalkboard has many lines drawn from where the two axes meet.
  • Dispersion
  • Phase Velocity
  • Group Velocity

Learning Objectives

By the end of this lecture, you should:

  • define a dispersive and non-dispersive medium and give examples.
  • combine two waves of approximately the same ω and k in a dispersive medium, to show the phase and group velocities.
  • describe the propagation of a wave in a dispersive medium.
  • define, and draw on an ω-k diagram, the slopes corresponding to the phase and group velocities.
  • understand why sharp features in a pulse cannot be supported in a dispersive medium.
  • know the speed of light and how to calculate wavelengths and frequencies of electromagnetic waves.
  • know that water and glass are dispersive media for electromagnetic waves.
  • graphically understand the dispersion relation of microwaves and the cutoff.

Lecture Activities

Check Yourself

  • Think about a 1 m deep circular swimming pool of 5 m radius, with vertical sides. Experience in tossing rocks into ponds suggests the wavelength of the resulting ripples is 5 cm and that they are in a packet. Describe, with some numbers, what happens if you throw a rock into the exact middle of the pool. Discuss times up to twice the time the wave packet takes to get to the outside rim.

› View/hide answer

With this wavelength, surface tension is unimportant and the water is deep compared to the wavelength Thus the dispersion relation is \(\omega = \sqrt {gk}.\) Since \( k = \frac{{2\pi }}{\lambda }\)we have \[k = \frac{{2\pi }}{{0.05}} = 126m^{-1}.\] In turn the frequency in Hz is \[\frac{\omega }{{2\pi }} = \frac{{\sqrt {gk} }}{{2\pi }} = \frac{{\sqrt {9.8(126)} }}{{2\pi }} = 5.6Hz.\] The ripples move at the phase speed which is \[{v_p} = \sqrt {\frac{g}{k}} = \sqrt {\frac{{9.8}}{{126}}} = 0.28 m/s\] (seems about right for those who have done this). The group speed is half this or \[{v_g} = 0.14 m/s. \] In \(\frac{5}{{.14}} = 36 s\) the pulse gets to the edge and since the boundary is free "a mountain comes back as a valley". After about one minute the pulse would get back to the middle and make a peak again.

 

  • Make a sketch graph showing the dispersion relation of deep water waves. For k = 100, draw on the lines allowing you to determine the phase and group speeds, and see if the slope of the latter really looks like half the slope of the former.

› View/hide answer

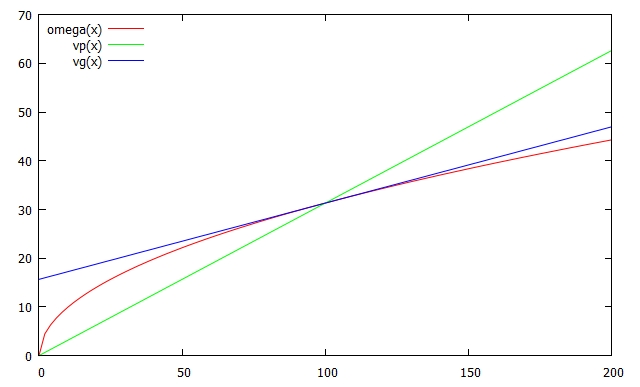
The function to be plotted is \(\omega = \sqrt {gk} = \sqrt {9.8k} = 3.13\sqrt k.\) When \(k = 100, \omega = 31.3 rad/s.\) The phase speed is \(\frac{\omega }{k} = 0.313 m/s\), which is the slope of the line from the origin \(\omega = 0.313k\). The tangent line at that point has a slope which can be approximated graphically or calculated exactly using \({d\Omega/dk}\) which is \( 3.13/{2 \sqrt{k}} \) . When k=100, this gives 0.1565 m/s, exactly half the speed, so its equation is \[\omega = 31.3 + 0.1565(k - 100)\] All comes out looking consistent.

Quiz12.jpg

 

« Previous | Next »