Statistical Optics...
... is the study of randomness in Optical Waves. In most introductory classes, we treat Optical Waves as deterministic quantities, described by electric and magnetic fields that obey Maxwell's Equations. This treatment is sufficient for forming the foundation of understanding Optical phenomena. However, a wealth of additional phenomena and applications can be discovered by taking the next step of re-formulating optical fields as statistical entities. Quantum physicists were the first to discover that the haven of determinism, while comfortable for lawful citizens averse to gambling, is still much deprived in terms of successfully describing Nature. Randomness is apparent all around us, and dominates the micro- and nano-scales where optical phenomena originate (light-matter interactions typically occur at the scale of wavelengths, ~0.5 micrometer for visible light). We will not venture into the quantum world in this class; instead, we will formulate Statistical Optics based on classical, phenomenological models sufficient to describe randomness for our purposes. We will use the standard formulation of stochastic processes to describe Random Optical Fields, and the Fourier Optics approach of block-diagram models of optical elements (except with random inputs).
What do I gain by learning Statistical Optics?
- Deep understanding of optics, since the simple, deterministic concepts are significantly reinforced when seen "belly-up" from the statistical point of view.
- Insight into other random processes in Nature, e.g. random mechanical/structural vibrations, noise in electrical circuits, etc. Not surprisingly, the formulations and properties among these diverse topics are essentially identical.
- Proficiency in cutting edge applications of Optics, primarily in imaging (but also in communications and computing). The traditional models of image formation (e.g., geometrically faithful and focus-conscious design of multi-element lens systems) are rapidly collapsing under the progress of optical science and fast, affordable digital processing. Statistical optics has led this revolution because it exploits the properties of Optical Fields in ways richer than either Geometrical or (deterministic) Wave Optics. Two examples of novel, unconventional imaging instruments are given below.

Very Large Array (VLA) Radio Telescope. (Image courtesy of the National Radio Astronomy Observatory.)
The VLA in Socorro, NM, utilizes 27 antennae with an overall aperture between 1.3km and 13km to observe very distant stars and galaxies. The mathematical foundation of the VLA's operation is the van Cittert-Zernicke theorem which allows us to associate the statistical autocorrelation between radio signals received at different antennae (pair-wise) with the structure of the remote radiowave sources.
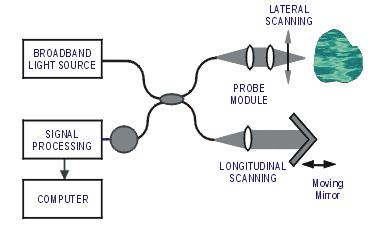
Optical Coherence Tomography (OCT). (Image courtesy of LightLab Imaging LLC. Used with permission.)
OCT is a non-invasive medical imaging technique which exploits the coherence properties of light to obtain depth information about tissue. It is based on "white light interferometry," a term which at first may sound like a contradiction (how can white light interfere?). When properly exploited, white light interference can provide excellent depth resolution (better than 1 micron) and decent lateral resolution (~10-30 microns, limited by the irregularities of the tissue).
