The motion of a narrow banded wave group can be regarded as a simusoidal wavetrain (blue dotted line) with central frequency and wave number, while the envelope (red solid line) is slowly varying in space and time. The speed of the envelope is called group velocity. The periodic variation of the envelope in space forms many wave packets. The group velocity is just the speed of these wave packets. From the dynamics view, group velocity has a physical significance-- the rate of energy transport, which makes it more important than the phase velocity.
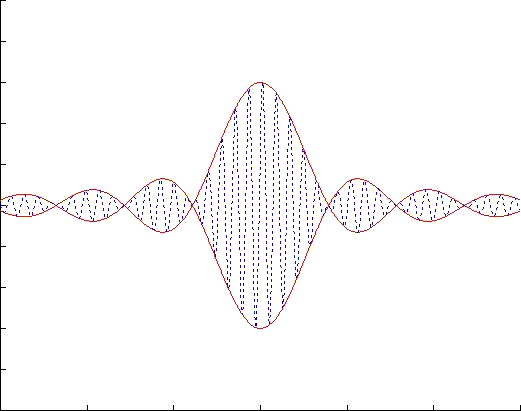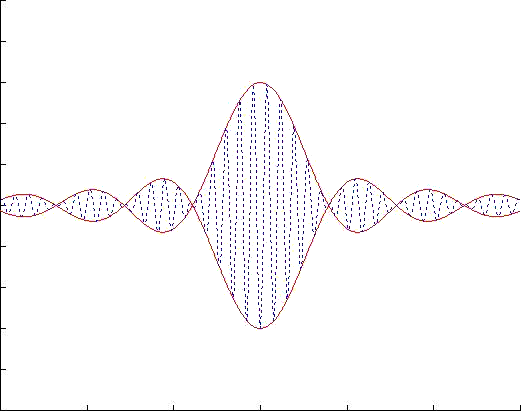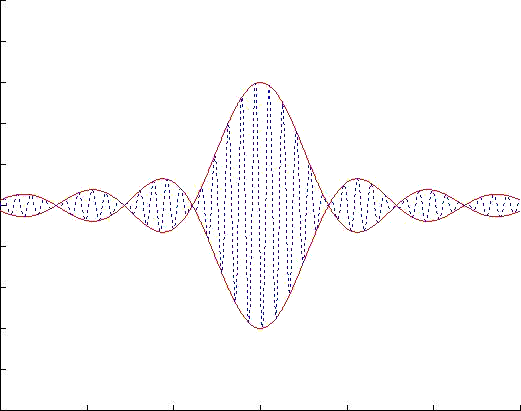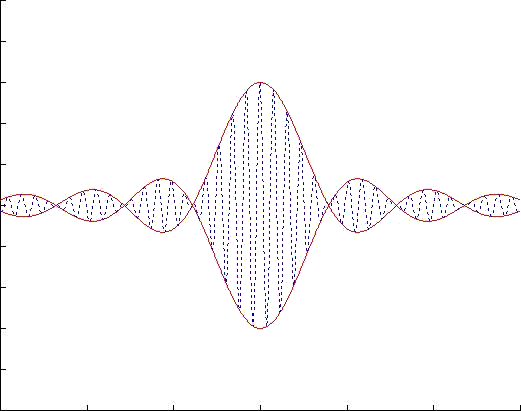
Image of MATLAB® software.
Our simulation above is under a reference frame moving with the group velocity. We can see that the carrying waves move from behind and vanish in the front of a wave packet since the phase velocity is greater than the group velocity.
