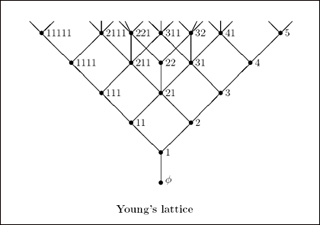
Young's lattice Y, the poset of all partitions of all nonnegative integers, ordered by containment of their Young diagrams. (Image by Prof. Richard Stanley.)
Instructor(s)
Prof. Richard Stanley
MIT Course Number
18.318
As Taught In
Spring 2006
Level
Graduate
Course Description
Course Features
Course Description
The course consists of a sampling of topics from algebraic combinatorics. The topics include the matrix-tree theorem and other applications of linear algebra, applications of commutative and exterior algebra to counting faces of simplicial complexes, and applications of algebra to tilings.


