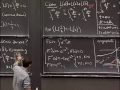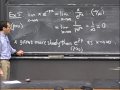Flash and JavaScript are required for this feature.
Download the video from iTunes U or the Internet Archive.
Topics covered: Exponential and log - Logarithmic differentiation; hyperbolic functions
Note: More on "exponents continued" in lecture 7
Instructor: Prof. David Jerison

Lecture 6: Exponential and Log
Related Resources
Lecture Notes (PDF)
The following content is provided under a Creative Commons License. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation, or to view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.
PROFESSOR: All right, so let's begin lecture six. We're talking today about exponentials and logarithms. And these are the last functions that I need to introduce, the last standard functions that we need to connect with calculus, that you've learned about. And they're certainly as fundamental, if not more so, than trigonometric functions.
So first of all, we'll start out with a number, a, which is positive, which is usually called a base. And then we have these properties that a to the power 0 is always 1. That's how we get started. And a^1 is a. And of course a^2, not surprisingly, is a times a, etc. And the general rule is that a^(x_1 + x_2) is a^(x_1) times a^(x_2). So this is the basic rule of exponents, and with these two initial properties, that defines the exponential function. And then there's an additional property, which is deduced from these, which is the composition of exponential functions, which is that you take a to the x_1 power, to the x_2 power. Then that turns out to be a to the x_1 times x_2. So that's an additional property that we'll take for granted, which you learned in high school.
Now, in order to understand what all the values of a^x are, we need to first remember that if you're taking a rational power that it's the ratio of two integers power of a. That's going to be a^m, and then we're going to have to take the nth root of that. So that's the definition. And then, when you're defining a^x, so a^x is defined for all x by filling in. So I'm gonna use that expression in quotation marks, "filling in" by continuity. This is really what your calculator does when it gives you a to the power x, because you can't even punch in the square root of x. It doesn't really exist on your calculator. There's some decimal expansion. So it takes the decimal expansion to a certain length and spits out a number which is pretty close to the correct answer. But indeed, in theory, there is an a to the power square root of 2, even though the square root of 2 is irrational. And there's a to the pi and so forth.
All right, so that's the exponential function, and let's draw a picture of one. So we'll try, say y = 2^x here. And I'm not going to draw such a careful graph, but let's just plot the most important point, which is the point (0,1). That's 2^0, which is 1. And then maybe we'll go back up here to -1 here. And 2 to the -1 is this point here. This is (-1, 1/2), the reciprocal. And over here, we have 1, and so that goes all the way up to 2. And then exponentials are remarkably fast. So it's off the board what happens next out at 2. It's already above my range here, but the graph looks something like this. All right. Now I've just visually, at least, graphically filled in all the rest of the points. You have to imagine all these rational numbers, and so forth. So this point here would have been (1, 2). And so forth.
All right? So that's not too far along. So now what's our goal? Well, obviously we want to do calculus here. So our goal, here, for now - and it's gonna take a while. We have to think about it pretty hard. We have to calculate what this derivative is.
All right, so we'll get started. And the way we get started is simply by plugging in the definition of the derivative. The derivative is the limit as delta x goes to 0 of a to the x plus delta x, minus a to the x, divided by delta x. So that's what it is. And now, the only step that we can really perform here to make this is into something a little bit simpler is to use this very first rule that we have here. That the exponential of the sum is the product of the exponentials. So we have here, a^x . So what I want to use is just the property that a^(x + delta x) = a^x a^(delta x). And if I do that, I see that I can factor out a common factor in the numerator, which is a^x. So we'll write this as the limit as delta x goes to 0, of a to the x times this ratio, now a to the delta x, minus 1, divided by delta x.
So far, so good? We're actually almost to some serious progress here. So there's one other important conceptual step which we need to understand. And this is a relatively simple one. We actually did this before, by the way. We did this with sines and cosines. The next thing I want to point out to you is that you're used to thinking of x as being the variable. And indeed, already we were discussing x as being the variable and a as being fixed. But for the purposes of this limit, there's a different variable that's moving. x is fixed and delta x is the thing that's moving. So that means that this factor here, which is a common factor, is constant. And we can just factor it out of the limit. It doesn't affect the limit at all. A constant times a limit is the same as whether we multiply before or after we take the limit. So I'm just going to factor that out. So that's my next step here. a^x, and then I have the limit delta x goes to 0 of a to the delta x minus 1, divided by delta x.
All right? And so what I have here, so this is by definition the derivative. So here is d/dx of a^x, and it's equal to this expression here. Now, I want to stare at this expression, and see what it's telling us, because it's telling us as much as we can get so far, without some-- So first let's just look at what this says. So what it's saying is that the derivative of a^x is a^x times something that we don't yet know. And I'm going to call this something, this mystery number, M(a). So I'm gonna make the label, M(a) is equal to the limit as delta x goes to 0 of a to the delta x minus 1 divided by delta x. All right? So this is a definition. So this mystery number M(a) has a geometric interpretation, as well. So let me describe that. It has a geometric interpretation, and it's a very, very significant number. So let's work out what that is. So first of all, let's rewrite the expression in the box, using the shorthand for this number. So if I just rewrite it, it says d/dx of a^x is equal to this factor, which is M(a), times a^x. So the derivative of the exponential is this mystery number times a^x.
So we've almost solved the problem of finding the derivative of a^x. We just have to figure out this one number, M(a), and we get the rest. So let me point out two more things about this number, M(a). So first of all, if I plug in x = 0, that's going to be d/dx of a^x , at x = 0. According to this formula, that's M(a) times a^0, which of course M(a). So what is M(a)? M(a) is the derivative of this function at 0. So M(a) is the slope of a^x at x = 0, of the graph. The graph of a^x at 0.
So again over here, if you looked at the picture. I'll draw the one tangent line in here, which is this one here. And this thing has slope, what we're calling M(2). So, if I graph the function y = 2^x, I'll get a certain slope here. If I graph it with a different base, I might get another slope. And what we got so far is the following phenomenon: if we know this one number, if we know the slope at this one place, we will be able to figure out the formula for the slope everywhere else. Now, that's actually exactly the same thing that we did for sines and cosines. We knew the slope of the sine and the cosine function at x = 0. The sine function had slope 1. The cosine function had slope 0. And then from the sum formulas, well that's exactly this kind of thing here, from the sum formulas. This sum formula, in fact is easier than the ones for sines and cosines. From the sum formulas, we worked out what the slope was everywhere. So we're following the same procedure that we did before. But at this point we're stuck. We're stuck, because that time using radians, this very clever idea of radians in geometry, we were able to actually figure out what the slope is. Whereas here, we're not so sure, what M(2) is, for instance. We just don't know yet.
So, the basic question that we have to deal with right now is what is M(a)? That's what we're left with. And, the curious fact is that the clever thing to do is to beg the question. So we're going to go through a very circular route here. That is circuitous, not circular. Circular is a bad word in math. That means that one thing depends on another, and that depends on it, and maybe both are wrong. Circuitous means, we're going to be taking a roundabout route. And we're going to discover that even though we refuse to answer this question right now, we'll succeed in answering it eventually. All right? So how are we going to beg the question? What we're going to say instead is we're going to define a mystery base, or number e, as the unique number, so that M(e) = 1. That's the trick that we're going to use. We don't yet know what e is, but we're just going to suppose that we have it.
Now, I'm going to show you a bunch of consequences of this, and also I have to persuade you that it actually does exist. So first, let me explain what the first consequence is. First of all, if M(e) is 1, then if you look at this formula over here and you write it down for e, you have something which is a very usable formula. d/dx of e^x is just e^x. All right, so that's an incredibly important formula which is the fundamental one. It's the only one you have to remember from what we've done. So maybe I should have highlighted it in several colors here. That's a big deal. Very happy.
And again, let me just emphasize, also that this is the one which at x = 0 has slope 1. That's the way we defined it, alright? So if you plug in x = 0 here on the right hand side, you got 1. Slope 1 at x = 0. So that's great. Except of course, since we don't know what e is, this is a little bit dicey.
So, next even before explaining what e is... In fact, we won't get to what e really is until the very end of this lecture. But I have to persuade you why e exists. We have to have some explanation for why we know there is such a number. Okay, so first of all, let me start with the one that we supposedly know, which is the function 2^x. We'll call it f(x) is 2^x. All right? So that's the first thing. And remember, that the property that it had, was that f'(0) was M(2). That was the derivative of this function, the slope at x = 0 of the graph. Of the tangent line, that is.
So now, what we're going to consider is any kind of stretching. We're going to stretch this function by a factor k. Any number k. So what we're going to consider is f(kx). If you do that, that's the same as 2^(kx). Right? But now if I use the second law of exponents that I have over there, that's the same thing as 2 to the k to the power x, which is the same thing as some base b^x, where b is equal to-- Let's write that down over here. b is 2^k. Right. So whatever it is, if I have a different base which is expressed in terms of 2, of the form 2^k, then that new function is described by this function f(kx), the stretch.
So what happens when you stretch a function? That's the same thing as shrinking the x axis. So when k gets larger, this corresponding point over here would be over here, and so this corresponding point would be over here. So you shrink this picture, and the slope here tilts up. So, as we increase k, the slope gets steeper and steeper. Let's see that explicitly, numerically, here. Explicitly, numerically, if I take the derivative here... So the derivative with respect to x of b^x, that's the chain rule, right? That's the derivative with respect to x of f(kx), which is what? It's k times f'(kx). And so if we do it at 0, we're just getting k times f'(0), which is k times this M(2).
So how is it exactly that we cook up the right base b? So b = e when k = 1 over this number. In other words, we can pick all possible slopes that we want. This just has the effect of multiplying the slope by a factor. And we can shift the slope at 0 however we want, and we're going to do it so that the slope exactly matches 1, the one that we want. We still don't know what k is. We still don't know what e is. But at least we know that it's there somewhere.
Yes?
Student: How do you know it's f(kx)?
PROFESSOR: How do I know? Well, f(x) is 2^x. If f(x) is 2^x, then the formula for f(kx) is this. I've decided what f(x) is, so therefore there's a formula for f(kx). And furthermore, by the chain rule, there's a formula for the derivative. And it's k times the derivative of f. So again, scaling does this. By the way, we did exactly the same thing with the sine and cosine function. If you think of the sine function here, let me just remind you here, what happens with the chain rule, you get k times cosine k t here. So the fact that we set things up beautifully with radians that this thing is, but we could change the scale to anything, such as degrees, by the appropriate factor k. And then there would be this scale factor shift of the derivative formulas. Of course, the one with radians is the easy one, because the factor is 1. The one with degrees is horrible, because the factor is some crazy number like 180 over pi, or something like that. Okay, so there's something going on here which is exactly the same as that kind of re-scaling.
So, so far we've got only one formula which is a keeper here. This one. We have a preliminary formula that we still haven't completely explained which has a little wavy line there. And we have to fit all these things together. Okay, so now to fit them together, I need to introduce the natural log. So the natural log is denoted this way, ln(x). So maybe I'll call it a new letter name, we'll call it w = ln x here. But if we were reversing things, if we started out with a function y = e^x , the property that it would have is that it's the inverse function of e^x. So it has the property that the log of y is equal to x. Right? So this defines the log.
Now the logarithm has a bunch of properties and they come from the exponential properties in principle. You remember these. And I'm just going to remind you of them. So the main one that I just want to remind you of is that the logarithm of x_1 * x_2 is equal to the logarithm of x_1 plus the logarithm of x_2. And maybe a few more are worth reminding you of. One is that the logarithm of 1 is 0. A second is that the logarithm of e is 1. All right? So these correspond to the inverse relationships here. If I plug in here, x = 0 and x = 1. If I plug in x = 0 and x = 1, I get the corresponding numbers here: y = 1 and y = e. And maybe it would be worth it to plot the picture once to reinforce this. So here I'll put them on the same chart. If you have here e^x over here. It looks like this. Then the logarithm which I'll maybe put in a different color. So this crosses at this all-important point here, (0,1). And now in order to figure out what the inverse function is, I have to take the flip across the diagonal x = y. So that's this shape here, going down like this. And here's the point (1, 0). So (1, 0) corresponds to this identity here. But the log of 1 is 0.
And notice, so this is ln x, the graph of ln x. And notice it's only defined for x positive, which corresponds to the fact that e^x is always positive. So in other words, this white curve is only above this axis, and the orange one is to the right here. It's only defined for x positive.
Oh, one other thing I should mention is the slope here is 1. And so the slope there is also going to be 1. Now, what we're allowed to do relatively easily, because we have the tools to do it, is to compute the derivative of the logarithm. So to find the derivative of a log, we're going to use implicit differentiation. This is how we find the derivative of any inverse function. So remember the way that works is if you know the derivative of the function, you can find the derivative of the inverse function. And the mechanism is the following: you write down here w = ln x. Here's the function. We're trying to find the derivative of w. But now we don't know how to differentiate this equation, but if we exponentiate it, so that's the same thing as e^w = x. Because let's just stick this in here. e^(ln x) = x. Now we can differentiate this. So let's do the differentiation here. We have d/dx e^w is equal to d/dx x, which is 1. And then this, by the chain rule, is d/dw of e^w times dw/dx. The product of these two factors. That's equal to 1. And now this guy, the one little guy that we actually know and can use, that's this guy here. So this is e^w times dw/dx, which is 1.
And so finally, dw/dx = 1 / e^w . But what is that? It's x. So this is 1/x. So what we discovered is, and now I get to put another green guy around here, is that this is equal to 1/x. So alright, now we have two companion formulas here. The rate of change of ln x is 1/x. And the rate of change of e^x is itself, is e^x. And it's time to return to the problem that we were having a little bit of trouble with, which is somewhat not explicit, which is this M(a) times x. We want to now differentiate a^x in general, not just e^x .
So let's work that out, and I want to explain it in a couple of ways, so you're going to have to remember this, because I'm going to erase it. But what I'd like you to do is, so now I want to teach you how to differentiate basically any exponential. So now to differentiate any exponential. There are two methods. They're practically the same method. They have the same amount of arithmetic. You'll see both of them, and they're equally valuable. So we're going to just describe them. Method one I'm going to illustrate on the function a^x. So we're interested in differentiating this thing, exactly this problem that I still didn't solve yet. Okay?
So here it is. And here's the procedure. The procedure is to write, so the method is to use base e, or convert to base e. So how do you convert to base e? Well, you write a^x as e to some power. So what power is it? It's e to the power ln a, to the power x. And that is just e^(x ln a). So we've made our conversion now to base e. The exponential of something. So now I'm going to carry out the differentiation. So d/dx of a^x is equal to d/dx of e^(x ln a).
And now, this is a step which causes great confusion when you first see it. And you must get used to it, because it's easy, not hard. Okay? The rate of change of this with respect to x is, let me do it by analogy here. Because say I had e^(3x) and I were differentiating it. The chain rule would say that this is just 3, the rate of change of 3x with respect to x times e^(3x). The rate of change of e to the u with respect to u. So this is the ordinary chain rule. And what we're doing up here is exactly the same thing, because ln a, as frightening as it looks, with all three letters there, is just a fixed number. It's not moving. It's a constant. So the constant just accelerates the rate of change by that factor, which is what the chain rule is doing.
So this is equal to ln a times e^(x ln a). Same business here with ln a replacing 3. So this is something you've got to get used to in time for the exam, for instance, because you're going to be doing a million of these. So do get used to it. So here's the formula. On the other hand, this expression here was the same as a^x. So another way of writing this, and I'll put this into a box, but actually I never remember this particularly. I just re-derive it every time, is that the derivative of a^x is equal to (ln a) a^x . Now I'm going to get rid of what's underneath it. So this is another formula.
So there's the formula I've essentially finished here. And notice, what is the magic number? The magic number is the natural log of a. That's what it was. We didn't know what it was in advance. This is what it is. It's the natural log of a. Let me emphasize to you again, something about what's going on here, which has to do with scale change. So, for example, the derivative with respect to x of 2^x is (ln 2) 2^x. The derivative with respect to x, these are the two most obvious bases that you might want to use, is ln 10 times 10^x . So one of the things that's natural about the natural logarithm is that even if we insisted that we must use base 2, or that we must use base 10, we'd still be stuck with natural logarithms. They come up naturally. They're the ones which are independent of our human construct of base 2 and base 10. The natural logarithm is the one that comes up without reference. And we'll be mentioning a few other ways in which it's natural later.
So I told you about this first method, now I want to tell you about a second method here. So the second is called logarithmic differentiation. So how does this work? Well, sometimes you're having trouble differentiating a function, and it's easier to differentiate its logarithm. That may seem peculiar, but actually we'll give several examples where this is clearly the case, that the logarithm is easier to differentiate than the function. So it could be that this is an easier quantity to understand. So we want to relate it back to the function u. So I'm going to write it a slightly different way. Let's write it in terms of primes here. So the basic identity is the chain rule again, and the derivative of the logarithm, well maybe I'll write it out this way first. So this would be d ln u / du, times d/dx u. These are the two factors. And that's the same thing, so remember what the derivative of the logarithm is. This is 1/u. So here I have a 1/u, and here I have a du/dx. So I'm going to encode this on the next board here, which is sort of the main formula you always need to remember, which is that (ln u)' = u' / u. That's the one to remember here.
STUDENT: [INAUDIBLE].
PROFESSOR: The question is how did I get this step here? So this is the chain rule. The rate of change of ln u with respect to x is the rate of change of ln u with respect u, times the rate of change of u with respect to x. That's the chain rule.
So now I've worked out this identity here, and now let's show how it handles this case, d/dx a^x. Let's do this one. So in order to get that one, I would take u = a^x . And now let's just take a look at what ln u is. ln u = x ln a. Now I claim that this is pretty easy to differentiate. Again, it may seem hard, but it's actually quite easy. So maybe somebody can hazard a guess. What's the derivative of x ln a? It's just ln a. So this is the same thing that I was talking about before, which is if you've got 3x, and you're taking its derivative with respect to x here, that's just 3. That's the kind of thing you have. Again, don't be put off by this massive piece of junk here. It's a constant. So again, keep that in mind. It comes up regularly in this kind of question.
So there's our formula, that the logarithmic derivative is this. But let's just rewrite that. That's the same thing as u' / u, which is (ln u)' = ln a, right? So this is our differentiation formula. So here we have u'. u' is equal to u times ln a, if I just multiply through by u. And that's what we wanted. That's d/dx a^x is equal to ln a (I'll reverse the order of the two, which is customary) times a^x.
So this is the way that logarithmic differentiation works. It's the same arithmetic as the previous method, but we don't have to convert to base e. We're just keeping track of the exponents and doing differentiation on the exponents, and multiplying through at the end.
Okay, so I'm going to do two trickier examples, which illustrate logarithmic differentiation. Again, these could be done equally well by using base e, but I won't do it. Method one and method two always both work.
So here's a second example: again this is a problem when you have moving exponents. But this time, we're going to complicate matters by having both a moving exponent and a moving base. So we have a function u, which is, well maybe I'll call it v, since we already had a function u, which is x^x. A really complicated looking function here. So again you can handle this by converting to base e, method one. But we'll do the logarithmic differentiation version, alright? So I take the logs of both sides. And now I differentiate it. And now when I differentiate this here, I have to use the product rule. This time, instead of having ln a, a constant, I have a variable here. So I have two factors. I have ln x when I differentiate with respect to x. When I differentiate with respect to this factor here, I get that x times the derivative of that, which is 1/x. So, here's my formula. Almost finished. So I have here v' / v. I'm going to multiply these two things together. I'll put it on the other side, because I don't want to get it mixed up with ln(x+1), the quantity. And now I'm almost done. I have v' = v (1 + ln x), and that's just d/dx x^x = x^x (1 + ln x). That's it. So these two methods always work for moving exponents. So the next thing that I'd like to do is another fairly tricky example. And this one is not strictly speaking within calculus. Although we're going to use the tools that we just described to carry it out, in fact it will use some calculus in the very end. And what I'm going to do is I'm going to evaluate the limit as n goes to infinity of (1 + 1/n)^n.
So now, the reason why I want to discuss this is, is it turns out to have a very interesting answer. And it's a problem that you can approach exactly by this method. And the reason is that it has a moving exponent. The exponent n here is changing. And so if you want to keep track of that, a good way to do that is to use logarithms. So in order to figure out this limit, we're going to take the log of it and figure out what the limit of the log is, instead of the log of the limit. Those will be the same thing.
So we're going to take the natural log of this quantity here, and that's n ln(1 + 1/n). And now I'm going to rewrite this in a form which will make it more recognizable, so what I'd like to do is I'm going to write n, or maybe I should say it this way: delta x is equal to 1/n. So if n is going to infinity, then this delta x is going to be going to 0. So this is more familiar territory for us in this class, anyway. So let's rewrite it. So here, we have 1 over delta x. And then that is multiplied by ln(1 + delta x). So n is the reciprocal of delta x. Now I want to change this in a very, very minor way. I'm going to subtract 0 from it. So that's the same thing. So what I'm going to do is I'm going to subtract ln 1 from it. That's just equal to 0. So this is not a problem, and I'll put some parentheses around it.
Now you're supposed to recognize, all of a sudden, what pattern this fits into. This is the thing which we need to calculate in order to calculate the derivative of the log function. So this is, in the limit as delta x goes to 0, equal to the derivative of ln x. Where? Well the base point is x=1. That's where we're evaluating it. That's the x_0. That's the base value. So this is the difference quotient. That's exactly what it is. And so this by definition tends to the limit here.
But we know what the derivative of the log function is. The derivative of the log function is 1/x. So this limit is 1. So we got it. We got the limit. And now we just have to work backwards to figure out what this limit that we've got over here is. So let's do that. So let's see here. The log approached 1. So the limit as n goes to infinity of (1 + 1/n)^n. So sorry, the log of this. Yeah, let's write it this way. It's the same thing, as well, the thing that we know is the log of this. 1 plus 1 over n to the n. And goes to infinity. That's the one that we just figured out. But now this thing is the exponential of that. So it's really e to this power here. So this guy is the same as the limit of the log of the limit of the thing, which is the same as log of the limit. The limit of the log and the log of the limit are the same. log lim equals lim log.
Okay, so I take the logarithm, then I'm going to take the exponential. That just undoes what I did before. And so this limit is just 1, so this is e^1. And so the limit that we want here is equal to e. So I claim that with this step, we've actually closed the loop, finally. Because we have an honest numerical way to calculate e. The first. There are many such. But this one is a perfectly honest numerical way to calculate e. We had this thing. We didn't know exactly what it was. It was this M(e), there was M(a), the logarithm, and so on. We have all that stuff. But we really need to nail down what this number e is. And this is telling us, if you take for example 1 plus 1 over 100 to the 100th power, that's going to be a very good, perfectly decent anyway, approximation to e.
So this is a numerical approximation, which is all we can ever do with just this kind of irrational number. And so that closes the loop, and we now have a coherent family of functions, which are actually well defined and for which we have practical methods to calculate.
Okay, see you next time.
Free Downloads
Video
- iTunes U (MP4 - 106MB)
- Internet Archive (MP4 - 106MB)
Free Streaming
Subtitle
- English - US (SRT)