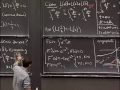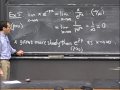Lecture 24: Numerical Integration

Related Resources

• Download this transcript - PDF (English - US)

The following content is provided under a Creative Commons license. Your support will help MIT OpenCourseWare continue to offer high quality educational resources for free. To make a donation or to view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu.

PROFESSOR: Today I want to get started by correcting a mistake that I made last time. And this was mistaken terminology. I said that what we were computing, when we computed in this candy bar example, was energy and not heat. But it's both. They're the same thing. And in fact, energy, heat and work are all the same thing in physics. I was foolishly considering the much more - what am I trying to say - the intuitive feeling of heat as just being the same as temperature. But in physics, usually heat is measured in calories and energy can be in lots of things. Maybe kilowatt-hours or ergs, these are various of the units. And work would be in things like foot-pounds. That is, lifting some weight some distance. And the amount of force you have to apply. And these all have conversions between them. They're all the same quantity, in different units. OK, so these are the same quantity. Different units. So that's about as much physics as we'll do for today. And sorry about that.

Now, the example that I was starting to discuss last time and that I'm going to carry out today was this dartboard example. We have a dartboard, which is some kind of target. And we have a person, your little brother, who's standing over there. And somebody is throwing darts. And the question is, how likely is he to be hit. So I want to describe to you how we're going to make this problem into a math problem. Yep.

STUDENT: [INAUDIBLE]

PROFESSOR: What topic is this that we're going over. We're going over an example. Which is a dartboard example. And it has to do with probability. OK. So what is the probability that this guy, your little brother, gets hit by a dart. Now, we have to put some assumptions into this problem in order to make it a math problem. And I'm really going to try to make them pretty realistic assumptions. So the first assumption is that the number of hits is proportional to some constant times e^(-r^2). So that's actually a kind of a normal distribution. That's the bell curve. But as a function of the radius. So this is the assumption that I'm going to make in this problem. And a problem in probability is a problem of the ratio of the part to the whole. So the part is where this little guy is standing. And the whole is all the possible places where the dart might hit. Which is maybe the whole blackboard or extending beyond, depending on how good an aim you think that this older child has. So, if you like, the part is-- We'll start simply. I mean, this doesn't sweep all the way around. But we're going to talk about some section. Like this. Where this is some radius r_1, and this other radius is some longer radius, r_2. And the part that we'll first keep track of is everything around there. That's not very well centered, but it's supposed to be two concentric circles. Maybe I should fix that a bit so that it's a little bit easier to read here. So here we go.

So here I have radius r_1, and here I have radius r_2. And then the region in between is what we're going to try to keep track of. So I claim that we'll be able to get-- So this is what I'm calling the part, to start out with. And then we'll take a section of it to get the place where the person is standing. Now, I want to take a side view of e^(-r^2). The function that we're talking about. Again, that's the bell curve. And it sort of looks like this. This is the top value, this is now the r-axis. And this is up, or at least-- So you should think of this in terms of the fact that the horizontal here is the plane of the dartboard. And the vertical is measuring how likely it is that there will be darts piling up here. So if they were balls tumbling down or something else falling on, many of them would pile up here. Many fewer of them would be piling up farther away. And the chunk that we're keeping track of is the chunk between r_1 and r_2. That's the corresponding region here. And in order to calculate this part, we have to calculate this volume of revolution. Sweeping around. Because really, in disguise, this is a ring. This is a side view, it's really a ring. Because we're rotating it around this axis here.

So we're trying to figure out what the total volume of that ring is. And that's going to be our weighting, our likelihood for whether the hits are occurring in this section, or in this ring, versus the rest. To set this up, I remind you we're going to use the method of shells. That's really the only one that's going to work here. And we want to integrate between r_1 and r_2. And the range here is that-- Because this is, if you like, a solid of revolution. So the variable r is the same as what we used to call x. And it's ranging between r_1 and r_2, and then we're sweeping it around. And the circumference of a little piece, so at a fixed distance r here, the circumference is going to be 2 pi r. So 2 pi r is the circumference. And then the height is the height of that green stem there. That's e^(-r^2). And then we're multiplying by the thickness, which is dr. So the thickness of the green is dr. The height of this little green guy is e^(-r^2), and the circumference is 2 pi times the radius, when we sweep the circle around. Question.

STUDENT: [INAUDIBLE]

PROFESSOR: So the question is, why is what we're interested in not this pink area. And the reason is an interpretation of what I meant by this. What I meant by this is that if you wanted to add up what the likelihood is that this thing will be here versus here, I want it to be, really, the proportions are the number of hits times the, if you like, I wanted it d area. That's really what I meant here. The number of hits in a little chunk. So little, maybe I'll call it delta A. A little chunk. Is proportional to the chunk times that. So there's already an area factor. And there's a height. So there are a total of three dimensions involved. There's the area and then this height. So it's a matter of the-- what I was given, what I intended to say the problem is. Yeah, another question.

STUDENT: [INAUDIBLE]

PROFESSOR: Yeah, yeah. Exactly. The height is c times that, whatever this c is. In fact, we don't know what the c is, but because we're going to have a part and a whole, we'll divide, the c will always cancel. So I'm throwing the c out. I don't know what it is, and in the end it won't matter. That's a very important question. Yes.

STUDENT: [INAUDIBLE]

PROFESSOR: Say it again?

STUDENT: PROFESSOR:

PROFESSOR: So what I mean is the number of hits in some chunk. That is, suppose you imagine, the question is, what does this left-hand side mean. That right? Is that the question that's you're asking? When I try to understand what the distribution of dartboard hits is, I should imagine my dartboard. And very often there'll be a whole bunch of holes in some places. And fewer holes else. I'm trying to figure out what the whole distribution of those marks is. And so some places will have more hits on them and some places will have fewer hits on them. And so what I want to measure is, on average, the number of hits. So this would really be some-- This constant of proportionality is ambiguous because it depends on how many times you try. If you throw a thousand times, it'll be much more densely packed. And if you have only a hundred times it'll be fewer. So that's where this constant comes in. But given that you have a certain number of times that you tried, say, a thousand times, there will be a whole bunch more piled in the middle. And fewer and fewer as you get farther away. Assuming that the person's aim is reasonable. So that's what we're saying. So we're thinking in terms of-- The person's always aiming for the center. So it's most likely that the person will hit the center. But on the other hand, it's a fallible person, so the person may miss. And so it's less and less likely as you go farther out. And we're just counting how many times this gets hit, how many time this and so on. In proportion to the area.

STUDENT: [INAUDIBLE]

PROFESSOR: Yeah. r_1 and r_2 are arbitrary. We're going to make this calculation in general. We're going to calculate what the likelihood is that we hit any possible band. And I want to leave those as just letters for now. The r_1 and the r_2. Because I want to be able to try various different possibilities.

STUDENT: [INAUDIBLE]

PROFESSOR: Say it again, why do we have to take volume? So this is what we were addressing before. It's a volume because it's number of hit per unit area. So there's a height, that is, number of hits. And then there's an area and the product of those is-- So this is, if you like, a histogram of the number of hits. But this should be measured per area. Not per length of r. Because on the real diagram, it's going all the way around. There's a lot more area to this red band than just the distance implies.

OK. So, having discussed the setup, this is a pretty standard setup-- Oh, one more question. Yes.

STUDENT: [INAUDIBLE]

PROFESSOR: Yeah. So the question is, why is this a realistic. Why is this choice of function here, e^(-r^2), a realistic choice of function for the darts. So I can answer this with an analogy. When people were asking themselves where the V-2 rockets from Germany hit London, they used this model. It turned out to be the one which was the most accurate. So that gives you an idea that this is actually real. The question, this makes it look like people are masters. That is, that they'll all hit in the center more often than elsewhere. But that's actually somewhat deceptive. There's a difference between the mode, that is, the most likely spot, and what happens on average. So in other words, the single most likely spot is the center. But there's rather little area in here, and in fact the likelihood of hitting that is some little tiny bit. In here. In fact, you're much more likely to be out here. So if you take the total of the volume, you'll see that much of the volume is contributed from out here. And in fact, the person hits rather rarely near the center. So this is not a ridiculous thing to do. If you think of it in terms of somebody's aiming at the center but there's some random thing which is throwing the person off, then there is likely to be to left or to the right, or they might even get lucky and all those errors cancel themselves and they happen to hit pretty much near the center. Yeah, another question.

STUDENT: [INAUDIBLE] PROFESSOR: How does the little brother come into play? The little brother is going to come into play as follows. I'll tell you in advance. So the thing is, the little brother was not so stupid as to stand in front of the target. I know. He stood about twice the radius of the target away. And so, we're going to approximate the location by some sector here. Which is just going to be some chunk of one of these things. We'll just break off a piece of it. And that's how we're going to capture. So the point is, the target is here. But there is the possibility that the seven-year-old who's throwing the darts actually missed the target. That actually happens a lot. So, does that answer your question? Alright. Are we ready now to to do this? One more question.

STUDENT: [INAUDIBLE]

PROFESSOR: I'm giving you this property here. I'm telling you that-- This is what's called a mathematical model, when you give somebody something like this. In fact, that requires further justification. It's an interesting issue. Yeah.

STUDENT: [INAUDIBLE]

PROFESSOR: I'm giving it to you for now. And it's something which really has to be justified. In certain circumstances it is justified. But, OK.

So anyway, here's our part. This is going to be our chunk, for now, that we're going to estimate the importance, the relative importance, of. And now, this is something whose antiderivative we can just do by substitution or by guessing. It's just -pi e^(-r^2). If you differentiate that, you get a -2r, which cancels the minus sign here. So you get 2pi r e^(-r^2). So that's the antiderivative. And we're evaluating it at r_1 and r_2. So with the minus sign that's going to get reversed. The answer is going to be pi times e^(-r_1^2), that's the bottom one, minus e^(r_2^2), that's the top. So this is what our part gives us. And, more technically, if you wanted to multiply through by c, it would be c times this. I'll say that in just a second.

OK, now I want to work-- So, if you like, the part is equal to, maybe even I'll call it c pi, times e^(-r_1^2) - e^(-r_2^2). That's what it really is if I put in this factor. So now there's no prejudice as to how many attempts we make. Whether it was a thousand attempts or a million attempts at the target. Now, the most important second feature here of these kinds of modeling problems is, there is always some kind of idealization. And the next thing that I want to discuss with you is the interpretation of the whole. That is, what's the family of all possibilities. And in this case, what I'm going to claim is that the reasonable way to think of the whole is it's that r can range all the way from 0 to infinity. Now, you may not like this. But these are maybe my first and third favorite number, my second favorite number being 1. So infinity is a really useful concept. Of course, it's nonsense in the context of the darts. Because if you think of the basement wall where the kid might miss a target, he'd probably hit the wall. He's probably not going to hit one of the walls to the right, and anyway he's certainly not going to hit over there. So there's something artificial about sending the possibility of hits all the way out to infinity. On the other hand, the shape of this curve is such that the real tail ends here, because of this exponential decrease, are tiny. And that's negligible. And the point is that actually the value, if you go all the way out to infinity, is the easiest value to calculate. So by doing this, I'm idealizing the problem but I'm actually making the numbers come out much more cleanly. And this is just always done in mathematics. That's what we did when we went from differences to differentials, to differentiation and infinitesimals. So we like that. Because it makes things easier, not because it makes things harder.

So we're just going to pretend the whole is from 0 to infinity. And now let's just see what it is. It's c pi times, the starting place is e^(-0^2). That's r_1, right, this is the role that r_1 plays is this, and the r_2 is this value. Minus e^(-infinity^2). Which is that negligibly small number, 0. So this is just c pi. Because this number is 1, and this other number is 0. This is just (1 - 0), in the parentheses there. And now I can tell you from these two numbers what the probability is. The probability that we landed on the target in a radius between r_1 and r_2, so that's this annulus here, is the ratio of the part to the whole. Which in this case just cancels the c pi. So it's e^(-r_1^2) - e^(-r_2^2). There's the formula for the probability. So the c canceled and the pi canceled. It's all gone.

Now, again, let me just emphasize the way this formula is supposed to work. The total probability of every possibility here is supposed to be set up to be 1. This is some fraction of 1. If you like, it's a percent. Yes.

STUDENT: [INAUDIBLE]

PROFESSOR: This one is giving-- The question is, doesn't this just give the probability of the ring? This gives you the probability of the ring, but this is a very, very wide ring. This is a ring starting with 0, nothing, on the inside. And then going all the way out. So that's everything. So this corresponds to everything. This corresponds to a ring.

So now, let's see. Where do I want to go from here. So in order to make progress here, I still have to give you one more piece of information. And this is, again, supposed to be realistic. When I was three years old and my brother's friend Ralph was seven, I watched him throwing darts a lot. And I would say that for Ralph, so for Ralph, at age seven, anyway, later on he got a little better at it. But Ralph at age seven, the probability that he hit the target was about 1/2. Right? So he hit the target about half the time. And the other times, there was cement on the walls of the basement, it wasn't that bad. Just bounced off. That also meant that the points got a little blunter as time went on. So it was a little less dangerous when they hit. Alright. So now, so here's the extra assumption that I want to make. So a is going to be the radius of the target. Now, the other realistic assumption that I want to make is where this little kid would be standing. And now, here, I want to get very specific and just do the computation in one case. We're going to imagine the target is here. And the kid is standing, say, between-- So we'll just do a section of this. This is between 3 o'clock and 5 o'clock. There's more of him, but it's lower down and maybe negligible here.

So this section is the part, the chunk that we want to see about. And this is a, and then this distance here is 2a. And then the longest distance here is 3a. So the longest distance is 3a. So in other words, what I'm saying is that the probability, if you're standing too close, the chance Ralph hits younger brother is about 1/6-- Right? Because 2/12 = 1/6. 1/6 of the probability that we're between a and 3a. That's the number that we're looking for. Another question.

STUDENT: [INAUDIBLE]

PROFESSOR: The 2/12 came from the fact that we assumed. So we made a very, very bold assumption here. We assumed that this human being, who is actually standing-- The floor is about down here. Maybe he wasn't that tall. But anyway, so he's really a little bigger than this. That the part of him that was close to the target covered about this section here, between radius 2a and 3a. As you'll see, actually from the computation, because the likelihood drops off pretty quickly, whatever of him was standing outside there wouldn't have mattered anyway. So we're just worried about the part that's closest to the target here.

STUDENT: [INAUDIBLE]

PROFESSOR: Why is it out of 12? Because I made it a clock. And I made it from 3 o'clock to 5 o'clock, so it's 2 of the 12 hours of a clock. It's just a way of me making a section that you can visibly see.

So now, so here's what we're trying to calculate. And in order to figure this out, I need one more item. here. So maybe I'll leave myself a little bit of room. I have to figure out something about what our information gave us. Which is that the probability, sorry, this probability was 1/2. So let's remember what this is. This is going to be e^(-0^2) - e^(-a^2). That's what's this probability is. And that's equal to 1/2. So that means that - 1 - e^(-a^2). = 1/2. Which means that e^(-a^2) = 1/2. I'm not going to calculate a, this is the part about the information about a that I want to use. That's what I'll use. And now I'm going to calculate this other probability here. So the probability right up there is this. And that's going to be the same as e^(-(2a)^2) - e^(-(3a)^2). That's what we calculated.

And now I want to use some of the arithmetic of exponents. This is (e^(-a^2))^2. Because it's really (2a)^2 is 4-- the quantity is 4a^2, and then I bring that exponent out. Minus e^(-a^2) to the 9th power, that's 3^2. And so this comes out to be (1/2)^4 - (1/2)^9. Which is approximately 1/16. This is negligible. This part here. And this is actually why these tails, as you go out to infinity, don't really matter that much. So this is a much smaller number. So the probability of the whole band is 1/16. And now I can answer the question up here. This is approximately 1/6 * 1/16. Which is about 1/100, or about 1%. So if I stood there for 100 attempts, then my chances of getting hit were pretty high. So that's the computation. That's a typical example of a problem in probability.

And let me just make one more connection with what we did before. This is connected to weighted averages or integrals over weights. But the weight that's involved in this problem was w(r) is equal to-- So let's just look at what happened in all of those integrals. What happened in all the integrals was, we had this factor here, 2 pi r. And if I include this c, it was really 2 pi c r e^(-r^2). This was the weight that we were using. The relative importance of things. Now, this is not the same as the e^(-r^2) that we started out with. Because this is the one-dimensional histogram. And that has to do with the method of shells that gave us that extra factor of r here. So that also connects with the question at the beginning, which had to do with this paradox, that it looks like these places in the middle are the most likely. But that's the plot e^(-r^2). If you actually look at this plot here, you see that as r goes to 0, it's going to 0. This is a different graph here. And actually, so this is what's happening really. In terms of how likely it is that you'll get within a certain distance of the center of the target. Again, it's not the area under that curve that we're doing. It's that volume of revolution. We're going to change subjects now. OK, one more question. Yes.

STUDENT: [INAUDIBLE]

PROFESSOR: Yeah, that's supposed to be the graph of w(r).

STUDENT: [INAUDIBLE]

PROFESSOR: Well, so, the question is, wouldn't the importance of the center be greatest? It's a question of which variable you're using. According to pure radius, it's not. It turns out that there are some bands in radius which are more important, more likely for hits than others. It really has to do with the fact that the center, or the core, of the target is really tiny. So it's harder to hit. Whereas a whole band around the outside has a lot more area. Many, many ways to hit that band. So it's a much larger area. So there's a competition there between those two things.

So we're going to move on. And I want to talk now about a different kind of weighted average. These weighted averages are going to be much simpler. And they come up in what's called numerical integration. There are many, many methods of integrating numerically. And they're important because many, many integrals don't have formulas. And so you have to compute them with a calculator or a machine. So the first type that we've already done are Riemann sums. They turned out to be incredibly inefficient. They're lousy.

The next rule that I'm going to describe is a little improvement. It's called the trapezoidal rule. And this one is much more reasonable than the Riemann sum. Unfortunately, it's actually also pretty lousy. There's another rule which is just a slightly trickier rule. And it's actually amazing that it exists. And it's called Simpson's Rule. And this one is actually pretty good. It's clever. So let's get started with these. And the way I'll get started is by reminding you what the Riemann sum is. So this is a good review, because you need to know all three of these. And you're going to want to see them all laid out in parallel.

So here's the setup. OK, so here we go. We have our graph, we have our function, it starts out at a, it ends up at b. Maybe goes on, but we're only paying attention to this interval. This is a function y = f(x). And we split it up when we do Riemann sums. So this is 1, this is Riemann sums. We start out with a, which is a point we call x_0, and then we go a certain distance. We go all the way over to b. And we subdivide this thing with these delta x's. Which are the step sizes. So we have these little steps of size delta x. Corresponding to these x values, we have y values. y_0 = f(x_0), that's the point above a. Then y_1 = f(x_1), that's the point above x_1. And so forth, all the way up to y_n, which is f(x_n). In order to figure out the area, you really need to know something about the function. You need to be able to evaluate it. So that's what we've done. We've evaluated here at n + 1 points. Enumerated 0 through n. And those are the numbers out of which we're going to get all of our approximations to the integral.

So somehow we want average these numbers. So here's our goal. Our goal is to average, or add, I'm using average very loosely here. But I was going to say add up these numbers to get an approximation. To average or add the y's. To get an approximation to the integral. Which we know is the area under the curve. So here's what the Riemann sum is. It's the following thing. You take y_0 plus y_1 plus... up to y_(n-1). And you multiply by delta x. That's it. Now, this one is the one with left endpoints. So the left-hand sum. There's also a right one. Which is, if you start at the right-hand ends. And that will go from y_1 to y_n. OK, so this one is the right-hand. Right Riemann sum. Those are the two that we did before. Now I'm going to describe to you the next two. They have a similar pattern to them. And the one with trapezoids requires a picture. Here's a shape. And here's a bunch of values. And we're trying to estimate the size of these chunks. And now, instead of doing something stupid, which is to draw horizontal lines in rectangles, we're going to do something slightly more clever. Which is to draw straight lines that are diagonal. You see that many of them actually coincide probably pretty closely with what I drew there. Although if they're curved, they miss by a little bit. So this is called the trapezoidal rule. Because if you pick one of these shapes, say this is y_2 and this is y_3, if you pick one of these shapes, this height here is y_2, and this height is y_3, and this base is delta x. This is a trapezoid.

So this being a trapezoid, I can figure out its area. And what do I get? I get the base times the average height. If you think about if, you work out what happens when you do something with a straight line on top, like that, you'll get this average. So this is the average height of the trapezoid. And now I want to add up. I want to add them all up to get my formula for the trapezoidal rule. So what do I do? I have delta x times the first one. Which is (y_0 + y_1) / 2. That's the first trapezoid. The next one is (y_1 + y_2) / 2. And this keeps on going. And at the end, I have (y_(n-2) + y_(n-1)) / 2. And then last of all, I have (y_(n-1) + y_n) / 2. That's a very long formula here. We're going to simplify it quite a bit in just a second. What's this equal to? Well, notice that I get y_0 / 2 to start out with.

And now, y_1 got mentioned twice. Each time with a factor of 1/2. So we get a whole y_1 in here. And the same thing is going to be true of all the middle terms. You're going to get y_2 and all the way up to y_(n-1). But then, the last one is unmatched. y_n is only 1/2, only counts 1/2. So here is what's known as the trapezoidal rule. Now, I'd like to compare it for you to the Riemann sums, which are sitting just to the left here. Here's the left one, and here's the right one. If you take the average of the left and the right, that is, a half of this plus a half of that, there's an overlap. The y_1 through y_n things are listed in both. But the y_0 only gets counted 1/2 and the y_n only gets counted 1/2. So what this is, is this is the symmetric compromise between the two Riemann sums. This is actually equal to the left Riemann sum plus the right Riemann sum divided by 2. It's the average of them.

Now, this would be great and it does look like it's closer. But actually it's not as impressive as it looks. If you actually do it in practice, it's not very efficient. Although it's way better than a Riemann sum, it's still not good enough. So now I need to describe to you the fancier rule. Which is known as Simpson's Rule. And so, this is, if you like, 3, Method 3. The idea is again to divide things into chunks. But now it always needs n to be even. In other words, we're going to deal not with just one box, we're going to deal with pairs of boxes. Here's delta x, and here's delta x again. And we're going to study the area of this piece here. So let me focus just on that part. Let's reproduce it over here.

And here's the delta x, here's delta x. And of course there are various heights. This starts out at y_0, this is y_2, and this middle segment is y_1. Now, the approximating curve that we're going to use is a parabola. That is, we're going to fit a parabola through these three points. And then we're going to use that as the approximating area. Now, it doesn't look like-- This looks like it misses. But actually, most functions mostly wiggle either one way or the other. They don't switch. They don't have inflection points. So, this is a lousy, at this scale. But when we get to a smaller scale, this becomes really fantastic. As an approximation. Now, I need to tell you what the arithmetic is. And in order to save time, it's on your problem set what the actual formula is. But I'm going to tell you how to think about it.

I want you to think about it as follows. So the area under the parabola is going to be a base times some kind of average height. And the base here, you can already see. It's 2 delta x. The base is 2 delta x. Now, the average height is weird. You have to work out what it is for a parabola, depending on those three numbers, y_0, y_1, and y_2. And it turns out to be the following formula. It has to be an average, but it's an interesting weighted average. So this was the punchline, if you like. Is that they are such things as interesting weighted averages. This one's very simple, it just involves three numbers. But it's still interesting. It's the following. It turns out to be (y_0 + 4y_1 + y_2) / 6. Why divided by 6? Well, it's supposed to be an average. So the total is 1 + 4 + 1 of these things. And 6 is in the denominator. So it emphasizes the middle more than the sides. And that's what happens with a parabola. So this is a computation which is on your homework. And now we can put this together for the full Simpson's Rule formula. Which I'll put up over here.

We have here 2 delta x, and we divide by 6. And then we have (y_0 + 4y_1 + y_2) / 6 plus-- That's the first chunk. Now, the second chunk, maybe I'll just put it in here, starts-- This is x_2. This is x_0. And it goes all the way to x_4. So x_2, x_3, x_4. So the next one involves the indices 2, 3 and 4. So this is (y_2 + 4y_3 + y_4) / 6. Oh, oh, oh, oh, no. I think I'll get rid of these 6's. I have too many 6's. Alright. Let's get rid of them here. Let's take them out. Put them out here. Thank you. All the way to the end, which is y_(n-2) plus 2y_(n-1)-- sorry, plus 4y_(n-1) plus y_n. I was about to divide by 6, but you saved me. So here are all the chunks.

Now, what does this pattern come out to be? This comes out to be the following. This is 1, 4, 1, added to 1, 4, 1 added to 1, 4, 1. You add them up. You get 1, 4, and then there's a repeat, so you get a 2 and a 4, and a 2 and a 4 and a 1. So the pattern is that it starts out with 1's on the far ends. And then 4's next in. And then it alternates 2's and 4's in between. So the full pattern of Simpson's Rule is delta x / 3, I have now succeeded in canceling this 2 with this 6 and getting out that factor of 2. And then here I have y0 + 4 y1 + 2 y2 + 4 y3 + ... It keeps on going and keeps on going and keeps on going. And in the end it's 2 y_(n - 2) + 4 y_(n - 1) + y_n. So again, 1 and a 4 to start. 4 and a 1 to end. And then alternating 2's and 4's in the middle. And this weird weighted average is way better. As I will show you next time.

Free Downloads

Video

• iTunes U (MP4 - 111MB)
• Internet Archive (MP4 - 111MB)

Free Streaming

• VideoLectures.net

Subtitle

• English - US (SRT)