Standing Waves Part II
Problem 1
An ideal taut string of length \( l \) and mass \( m \) is attached to a fixed point at one end and to a massive ring of mass \( M_R \) at the other end as shown below. The ring is free to move on a horizontal frictionless rod which is perpendicular to the string in its equiibrium position. The tension in the string, \( T \), can be considered constant at all times and gravity can be ignored.
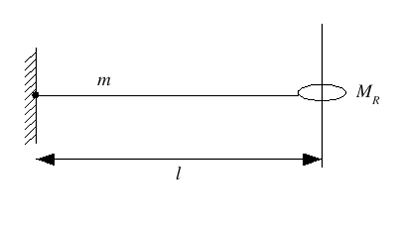
- Starting with the general form of the normal mode solutions of the classical wave equation for a taut string, derive an equation which, when solved, gives the angular frequency \( \omega \) of the lowest mode of the system. YOU ARE NOT ASKED TO SOLVE THIS EQUATION.
- Determine the angular frequency of the lowest normal mode for
- \( M_R = 0 \)
- \( M_R = \infty \).
- \begin{eqnarray} \nonumber \omega &=& \frac{T}{M_R}\sqrt{\frac{m}{Tl}}\cot \left( \omega l \sqrt{\frac{m}{Tl}}\right) \\ \nonumber &=& \frac{1}{M_R}\sqrt{\frac{Tm}{l}}\cot \left( \omega \sqrt{\frac{ml}{T}}\right) \end{eqnarray}
This is a transcendental equation with no simple solution.
- For \( M_R = 0 \), we get \begin{eqnarray} \nonumber &&\cot \left( \frac{\omega}{v}l\right) = 0 \hspace{3mm} with \hspace{3mm} v = \sqrt{\frac{Tl}{m}} \\ \nonumber &\Rightarrow& \frac{\omega}{v}l = \frac{\pi}{2} \\ \nonumber &\Rightarrow& \omega = \frac{\pi}{2l}v = \frac{\pi}{2l}\sqrt{\frac{Tl}{m}} = \frac{\pi}{2}\sqrt{\frac{T}{ml}} \end{eqnarray} for the lowest normal mode. Intuitively, this makes sense since this situation corresponds to a string which is fixed at one end and free at the other, so the lowest normal mode has \( l = \lambda / 4 \) or \( \lambda = 4l \) and thus \( \omega = \dfrac{2 \pi v}{\lambda} = \dfrac{2 \pi v}{4l} = \dfrac{\pi}{2l}v \).
- For \( M_R = \infty \), we get \begin{eqnarray} \nonumber &&\tan \left( \frac{\omega}{v}l\right) = 0 \\ \nonumber &\Rightarrow& \frac{\omega}{v}l = \pi \\ \nonumber &\Rightarrow& \omega = \frac{\pi}{l}v = \frac{\pi}{l}\sqrt{\frac{Tl}{m}} = \pi\sqrt{\frac{T}{ml}} \end{eqnarray} for the lowest normal mode. Intuitively, this makes sense since this situation corresponds to a string which is fixed at both ends, so the lowest normal mode has \( l = \lambda / 2 \) or \( \lambda = 2l \) and thus \( \omega = \dfrac{2 \pi v}{\lambda} = \dfrac{2 \pi v}{2l} = \dfrac{\pi}{l}v \).
Problem 2
A system consists of two materials glued together at \(x = L\) and subject to longitudinal (sound) wave propagation. The end at \(x = 0\) is fixed and the end at \(x = 4L\) is free. A tungsten-lead alloy is used for the segment \(0 \leq x \leq L\), with a Young's modulus of \(Y = 7 \times 10^{10}\) N/m\(^2\) and density \(\rho = 14.4 \times 10^{3}\) kg/m\(^3\), while the segment \(L \leq x \leq 4L\) is comprised of a carbon fiber alloy that is as strong as the tungsten-lead alloy with \(Y = 7 \times 10^{10}\) N/m\(^2\) but nine times less dense, with \(\rho = 1.6 \times 10^{3}\) kg/m\(^3\).
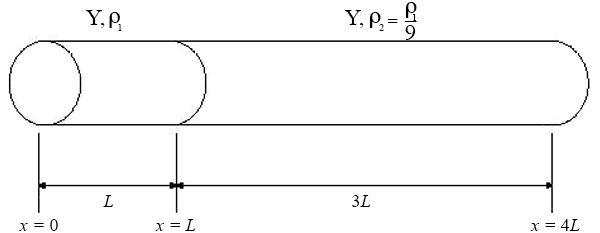
- Derive a condition for the normal mode frequency of longitudinal oscillation, \(\omega_n\), of the two-metal system.
- Evaluate the frequencies for the first four modes, in terms of the length \(L\).
The phase velocity \(v\) of longitudinal waves \( = \sqrt{\dfrac{Y}{\rho}}\)
\(\therefore \dfrac{v_2}{v_1} = 3\) and the essence of the problem is the boundary conditions at \(x\) = 0, \(L\) and \(4L\).
- \( sin{\dfrac{\omega_n L}{v_1}} = \pm \dfrac{\sqrt{3}}{2} \) with \(v_1 = \sqrt{\dfrac{Y_1}{\rho_1}} \approx 2.2 \times 10^{3}\) m/s
- \( \omega_1 = {\dfrac{v_1}{L}}{\dfrac{\pi}{3}} \); \( \omega_2 = {\dfrac{v_1}{L}}{\dfrac{2 \pi}{3}} \); \( \omega_3 = {\dfrac{v_1}{L}}{\dfrac{4 \pi}{3}} \); \( \omega_4 = {\dfrac{v_1}{L}}{\dfrac{5 \pi}{3}} \)
[Note that just about any factor other than 3 for speed and length ratios would give an equation which could not be easily solved.]
« Previous | Next »


