Description: ODE2 implements a midpoint method with two function evaluations per step. This method is twice as accurate as Euler's method. A nonlinear equation defining the sine function provides an example. An exercise involves implementing a related trapezoid method.
Related MATLAB code files can be downloaded from MATLAB Central
Instructor: Cleve Moler
PROFESSOR: The cost of a numerical method for solving ordinary differential equations is measured by the number of times it evaluates the function f per step. Euler's method evaluates f once per step. Here's a new method that evaluates it twice per step. If f is evaluated once at the beginning of the step to give a slope s1, and then s1 is used to take Euler's step halfway across the interval, the function is evaluated in the middle of the interval to give the slope s2. And then s2 is used to take the step. For obvious reasons, this is called the midpoint method.
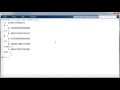
Here's ode2. It implements the midpoint method, evaluates the function twice per step. The structure is the same as ode1. Same arguments, same for loop, but now we have s1 at the beginning of the step, s2 in the middle of the step, and then the step is actually taken with s2.
Here's an example involving a trig function. Dy dt is the square root of 1, minus y squared. Starting at the origin on the interval from 0 to pi over 2. Now, because I've called it a trig example, you might just-- this is a separable equation-- do the integral, or you can just guess at the-- guess that the answer is sine t. Because the derivative of sine t is the cosine of t, and that's the square root of 1 minus y squared.
Let's set it up. F is the anonymous function square root of 1 minus y squared. T0 is 0. I'm going to take h to be pi over 32. And tfinal is pi over 2. And y0 is 0. And here's my call to ode2, with these five arguments, and it produces this output.
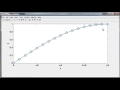
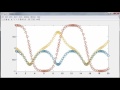
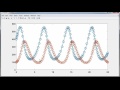
Now I want to plot it. Let's get t to go along with it. There is the t values as a column-- vector-- and let's plot. And do some annotation on the plot. Here's our plot. So there's the graph of our, there's the graph of sine t, the points generated by ode2.
Now I can't help but go look at these answers. This is supposed to be the values of sine t. This should be getting to 1 at pi over 2. We've got 0.997. That gives you a rough idea of what kind of accuracy we're getting out of this crude numerical method.
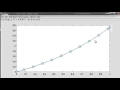
Let's take a look at an animation of the midpoint method. The differential equation is y prime is 2y, starting at t0 equals 0 with a step size of 1, going up to 3, and starting with y0 equals 10, and using ode2. Here is the animation. Here's t0 and y0. Evaluate the function at y0. 2 times y0 is 20, step halfway across the interval with that slope, that gets us to 20. Evaluate the function there, the slope is 40, so we take a step with slope 40 all the way across the interval to get up to 50.
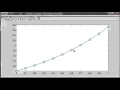
That's the first step. Now we'll rescale the plot window. Here we are at 50. Evaluate the function there. The slope is 100, step halfway with that slope, get to the middle of the interval, evaluate the function there. The slope is 200, so we take a step with slope 200 to get up to 250. That's the second step. Rescale the plot window. Evaluate the function there. The slope is 500. Take that step halfway across the interval, evaluate the slope there. The slope is 1,000, so we take a step with slope of 1,000 to get up to 1,250 as our final value.
Since this is a rapidly increasing function of y, the values we generate here with the midpoint method are far larger than the values generated with the Euler method that we saw with ode1.
Here's an exercise. Modify ode2, creating ode2t, which implements the companion method, the trapezoid method. Evaluate the function at the beginning of the interval to get s1. Use s1 to go all the way across the interval. Evaluate the function at the right-hand endpoint of the interval to get s2. And then, use the average of s1 and s2 to take the step. That's the trapezoid method.