(b) Michalske [1] predicted that water molecules assisted bond breaking in silica long before it was observed directly in atomistic simulations. In his 1984 paper, Fig. 6 is a little hard to understand at first. Make this the inset in a larger figure that shows a macroscopic crack, the direction of loading to open that crack in Mode I, and the direction of propagation of that crack.
Below is a larger figure that shows the macroscopic crack. The figure 6 is the one from Michalske's 1984 paper. It is an atomic view of the crack front separating severed from intact bonds.
The direction of loading during mode 1 is normal to the crack faces.
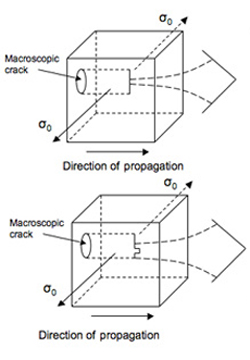
Portion of image removed due to copyright restrictions. Please see Fig. 6 in [1].
(c) Explain chemically assisted fracture so that anyone in 3.22 would understand it, using Michalske's Fig. 7 type graphics [1] to illustrate the interaction of water with silica at the molecular level.
Image removed due to copyright restrictions. Please see Fig. 7 in [1].
The diagram above shows an example of a chemically assisted fracture mechanism; in this case, how an active molecule (such as H2O or NH3) can assist the breaking of strained Si-O-Si bonds, ie. the kink on fig. 6 in question b. The steps are as follows:
- The initial silica surface, in the absence of applied strain.
- Under applied tension, silica initially responds by changing its conformation but retaining tetrahedral bond angles around the Si molecules.
- As the tension increases the Si-O-Si bonds elongate to form an angle of 180° around the bridging oxygens. This step is almost costless (4 kcal/mol) and has little effect on the bond reactivity.
- Finally, certain silicon atoms are forced to give up their tetrahedral molecular orbital configuration. In this strained state, the bridging Si-O-Si bond has a strongly increased reactivity.
- The Si-O-Si bond reacts with H2O and is cleaved into 2-OH terminal groups.
(d) Michalske's argument [1] necessarily implies that the amount of chemical in the environment affects the speed of crack growth. Assume an initial, through-thickness crack of width 150 nm at the surface of a sheet of silica that is 1 cm thick. The crack is under Mode I loading. From Michalske's Fig. 2, how long would it take for that crack to grow another 150 nm under an applied stress of 100 MPa in an environment of 100% water?
Image removed due to copyright restrictions. Please see Fig. 2 in [1].
In class we saw that the stress intensity KI in Mode I loading is calculated by
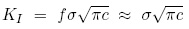
where c is the crack size and f is a factor close to unity. Using the crack size and stress values given, we get a value KI = 0.069 MPa m1/2. This value is out of the range of the data plots on the figure above, but by extrapolation we can estimate the crack propagation velocity to be 5 nm/s. It would thus take 30 s for the crack to grow another 150 nm.
(e) At a partial pressure of 50%, how many water molecules would be sitting on the initial crack faces?
Michalske [1] states that Si-O bonds are incapable of adsorbing environmental chemicals until the strain exceeds a certain critical level. We can therefore assume that at the initial stage, molecules will sit on the crack faces without any preference. At a partial pressure of 50%, half of the molecules sitting on the crack faces will be water molecules. The molar volume of an ideal gas at room temperature is Vm = 24.8 L/mol. Therefore, the number of molecules per unit area is: (Na /Vm)2/3 = 8.39*1016 /m2 where Na is the Avogadro number. On a crack surface of width 150 nm and thickness 1 cm, the number of water molecules is: 6.29*107 molecules.
Reference
[1] Michalske, T. A., and B. C. Bunker. "Slow Fracture Model Based on Silicate Fracture Models." Journal of Applied Physics 56 (November 15, 1984): 2686-2693.
Plasticity and fracture of microelectronic thin films/lines
Effects of multidimensional defects on III-V semiconductor mechanics
Defect nucleation in crystalline metals
Role of water in accelerated fracture of fiber optic glass | Problem Set 2 | Problem Set 3 | Problem Set 5
Carbon nanotube mechanics
Superelastic and superplastic alloys
Mechanical behavior of a virus
Effects of radiation on mechanical behavior of crystalline materials
