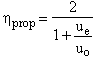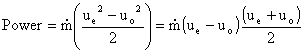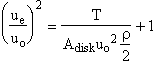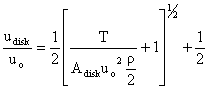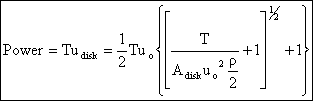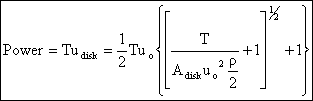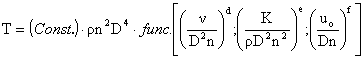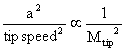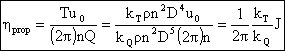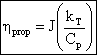VII. Production of Thrust with a Propeller
A.
Overview of propeller performance
Each propeller blade is a rotating airfoil which produces lift and drag,
and because of a (complex helical) trailing vortex system has an induced upwash
and an induced downwash.
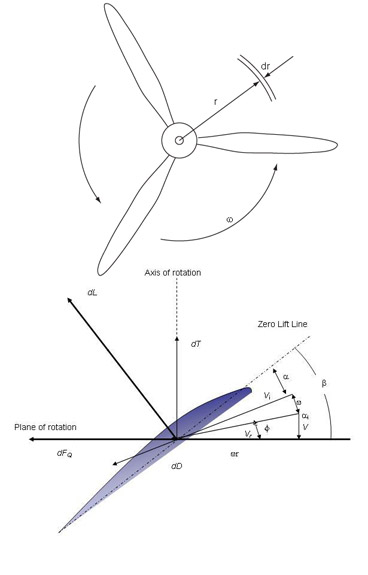
Figure 7.1 Adapted from
McCormick, 1979.
The two quantities of interest are the thrust (T) and the torque (Q). We
can write expressions for these for a small radial element (dr) on one of
the blades:
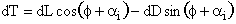
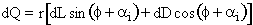
where
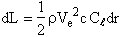 and
and 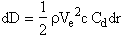
It is possible to integrate the relationships as a function of r with the
appropriate lift and drag coefficients for the local airfoil shape, but determining
the induced upwash (ai)
is difficult because of the complex helical nature of the trailing vortex
system. In order to learn about the details of propeller design, it is necessary
to do this. However, for our purposes, we can learn a about the overall performance
features using the integral momentum theorem, some further approximations
called “actuator disk theory”, and dimensional analysis.
NASA Glenn has a nice explanation of propeller
thrust - GO!
|
B. Application of the Integral Momentum Theorem to Propellers
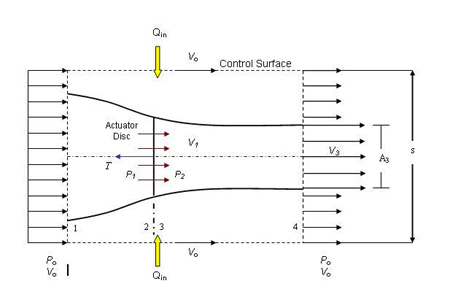
Figure 7.2 Adapted from
McCormick, 1979
The control volume shown in Figure 7.2 has been drawn far enough from
the device so that the pressure is everywhere equal to a constant. This is
not required, but it makes it more convenient to apply the integral momentum
theorem. We will also assume that the flow outside of the propeller streamtube
does not have any change in total pressure. Then since the flow is steady
we apply:
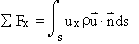
Since the pressure forces everywhere are balanced, then the only force on
the control volume is due to the change in momentum flux across its boundaries. Thus by inspection, we can say that
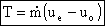
Or we can arrive at the same result in a step-by-step manner as we did for
the jet engine example in Section II:
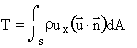
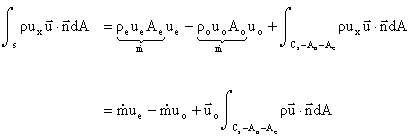
Note that the last term is identically equal to zero by conservation of mass. If the mass flow in and out of the propeller streamtube are the same (as we
have defined), then the net mass flux into the rest of the control volume
must also be zero.
So we have:
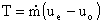
as we reasoned before.
The power expended is equal to the power imparted to the fluid which is the
change in kinetic energy of the flow as it passes through the propeller

The propulsive power is the rate at which useful work is done which is the
thrust multiplied by the flight velocity

The propulsive efficiency is then the ratio of these two:
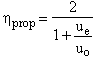
Which is the same expression as we arrived at before for the jet engine (as
you might have expected).
C.
Actuator Disk Theory
To understand more about the performance of propellers, and to relate
this performance to simple design parameters, we will apply actuator disk
theory. We model the flow through the propeller as shown in Figure 7.3 below
and make the following assumptions:
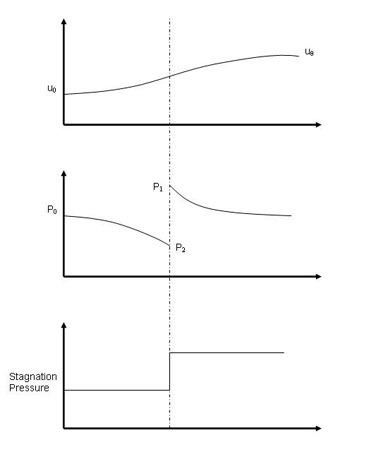
Figure 7.3 Adapted from
Kerrebrock.
We then take a control volume around the disk as shown in Figure 7.4
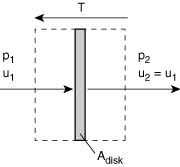
Figure 7.4 Control volume
around actuator disk.
The force, T, on the disk is
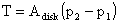
So the power is
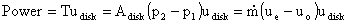
We also know that the power is
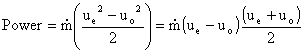
Thus we see that the velocity at the disk is
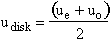
Half of the axial velocity change occurs upstream of the disk and half occurs
downstream of the disk.
We can now find the pressure upstream and downstream of the disk by applying
the Bernoulli equation in the regions of the flow where the pressure and velocity
are varying continuously.
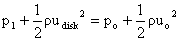 and
and 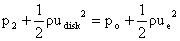
From which we can determine
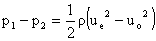
We generally don’t measure or control udisk directly. Therefore,
it is more useful to write our expressions in terms of flight velocity uo,
thrust, T, (which must equal drag for steady level flight) and propeller disk
area, Adisk.
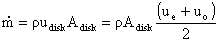
So
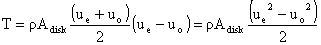
From which we can obtain an expression for the exit velocity in terms of
thrust and flight velocity which are vehicle parameters
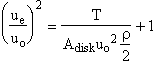
The other parameters of interest become
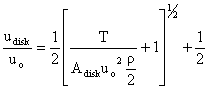
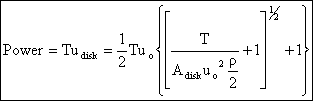
This is the ideal (minimum) power required to drive the propeller. In general , the actual power required would be about 15% greater than this.
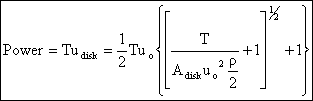
There are several important trends that are apparent upon consideration of
these equations. We see that the propulsive efficiency is zero when the flight
velocity is zero (no useful work, just a force), and tends towards one when
the flight velocity increases. In practice, the propulsive efficiency typically
peaks at a level of around 0.8 for a propeller before various aerodynamic
effects act to decay its performance as will be shown in the following section.
D. Dimensional Analysis
We will now use dimensional analysis to arrive at a few important
parameters for the design and choice of a propeller. Dimensional analysis
leads to a number of coefficients which are useful for presenting performance
data for propellers.
| Parameter
|
Symbol
|
Units
|
| propeller
diameter
|
D
|
m
|
| propeller
speed
|
n
|
rev/s
|
| torque
|
Q
|
Nm
|
| thrust
|
T
|
N
|
| fluid
density
|
r
|
kg/m3
|
| fluid
viscosity
|
n
|
m2/s
|
| fluid
bulk elasticity modulus
|
K
|
N/m2
|
| flight
velocity
|
uo
|
m/s
|
1.
Thrust Coefficient
T = f(D; n; r; n; K; uo)
= Const. Da nb rc
nd Ke uof
Then putting this in dimensional form
[MLT-2] = [(L)a(T)-b(ML-3)c(L2T-1)d(ML-1T-2)e(LT-1)f]
Which implies
(M)
1= c+ e
(L)
1 = a - 3c + 2d e + f
(T) 2 = b + d + 2e
+ f
So
a = 4 2e 2d f
b = 2 d 2e f
c = 1 - e
T = Const. D4-2e-2d-f n2-d-2e-f
r1-e nd Ke uof
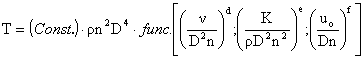
We can now consider the three terms in the square brackets
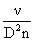 :
Dn is proportional to the tip speed, so this term is like
:
Dn is proportional to the tip speed, so this term is like 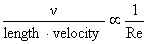
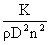 :
K/r = a2 where a is the
speed of sound, this is like
:
K/r = a2 where a is the
speed of sound, this is like 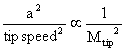
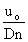 :
uo/n is the distance advanced by the propeller in one revolution,
here non-dimensionalized by the propeller diameter.
:
uo/n is the distance advanced by the propeller in one revolution,
here non-dimensionalized by the propeller diameter.
This last coefficient is typically called the advance
ratio and given the symbol J.
Thus we see that the thrust may be written as
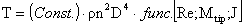
which is often expressed as
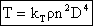 where kT is called the thrust coefficient and in general is a function
of propeller design, Re, Mtip and J.
where kT is called the thrust coefficient and in general is a function
of propeller design, Re, Mtip and J.
2. Torque Coefficient
We can follow the same steps to arrive at a relevant expression
and functional dependence for the torque or apply physical reasoning. Since
torque is a force multiplied by a length, it follows that
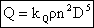 where kQ is called the thrust coefficient and in general is a function
of propeller design, Re, Mtip and J.
where kQ is called the thrust coefficient and in general is a function
of propeller design, Re, Mtip and J.
3.
Efficiency
The power supplied to the propeller is Pin where
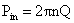
The useful power output is Pout where
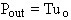
Therefore the efficiency is given by
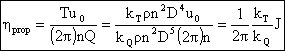
4.
Power Coefficient
The power required to drive the propeller is
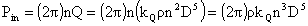
which is often written using a power coefficient Cp
= 2pkQ
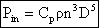 then
then 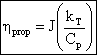
E. Typical propeller performance
Typical propellor performance curves can be found in McCormick, B.W.
Aerodynamics, Aeronautics, and Flight Mechanics. John Wiley & Sons
Inc. 1979.

![]()
![]()
![]() and
and ![]()

![]()
![]()
![]()
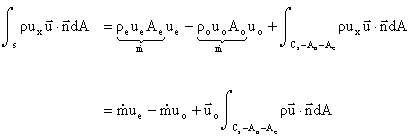
![]()

![]()